一种大型弹箭动平衡测量系统及设计 2011-05-25

0 引言
大型箭弹零部件在加工及装配过程中，总存在尺寸、形状及位置误差。这些误差的存在，使得装配后的火箭弹质心位置偏离全弹几何纵轴，且惯性主轴与几何纵轴不重合，即产生质量偏心距，静不平衡和动不衡度。由于各种加工、装配误差的或然性，使得每发火箭弹的质量偏心距和动不平衡角有不同的大小和相位，动静不平衡度的随机分布将会使火箭弹产生落点散布，其散布效应影响其飞行控制和命中精度。散布效应是飞行物体偏离其预定轨道的统计偏差。而其质量分布不均是引起其散布的重要原因，所以这类飞行物体的双面立式动平衡是测量其质量特性的关键一环。通过动平衡测试并建立空间坐标系，可以求出飞行物体的主惯性轴方程，进而可以求出其主惯性轴与几何形心轴线之间的夹角。通过了解飞行物体的质量特性，可以改进装配和加工工艺，可有效提高飞行物体弹道曲线控制精度。同时，弹箭动不平衡质量还影响弹丸膛内运动的正确性、膛壁的受力及其磨损，最终影响火炮寿命，因此测定弹箭动不平衡参数在弹箭弹道试验前是必须进行的。
但是，有的弹箭质量重、体积庞大，用通常的卧式旋转方法就无法实现，本文针对这种情况设计了一种立式的测量方法来实现大型重物的动平衡测量。

1 大型弹箭动平衡测量系统及设计
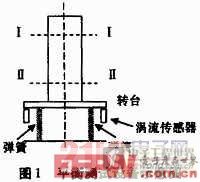
对于大型弹箭这类旋转物体，由于其没有转动支撑部位，不能采用常规的动平衡测量方法来进行校正，而且其允许的转速又很低，所以针对这种特殊性，设计一个转台，用过渡盘将工件和转台联结起来，用两根弹簧作为整套系统的弹性元件。当转台连同工件一起转动时，由弹簧来感受其不平衡量。在与弹簧相连的支架外端处安装二只电涡流传感器，将支架在转台转动时产生的振动位移信号转变为电信号进行测量。
把待测工件安装在平衡测试设备上，用涡流传感器监测弹簧的变形，并选定工件上I—I，Ⅱ一Ⅱ为校正平面(见图1)。在安装调整标定工作完成之后，启动设备以极低的转速稳定旋转。由于转速非常低，而工件不平衡产生的不平衡惯性力和惯性力矩与转速的平方成正比，故其近似为零。此时在工件上的静不平衡量是由重力偏心引起的，此时弹簧变形响应信号可以测出，重力的偏心距就可以得到了。

2 不平衡量的测量理论推导
由剐性转子二面平衡原理，可以假设下面的模型来推导不平衡量是怎样反映到输出波形上的。

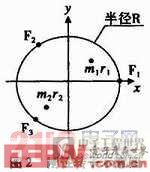
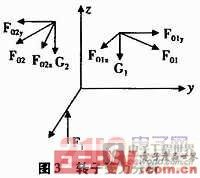
对一刚性转子，选二个校正面I、Ⅱ，离底面的高度分别为h1，h2，F1、F2、F3分别为均匀分布在半径为R的底面圆上三个点处所受的力。我们先假设该刚性转子是动平衡的，在预设的I、Ⅱ校正面r1，r2处放上两个质量块m1，m2，这样刚体便处于动不平衡了，当使这个不平衡的转子以一定的速度旋转时，对其进行受力分析如图2，其中F1，F2分别为旋转时质量块m1，m2所受的离心力，把它们分别沿X、Y轴方向进行分解，转子沿X、Y轴方向的转矩为零，Z轴方向合力为零，有如下的方程：

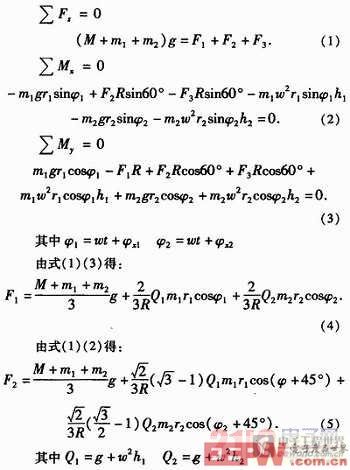
如果在受力F1，F2处分别安装上传感器，则振动位移信号通过传感器、放大电路、滤波电路、A／D转换等中间过程后，以电信号的形式输出，实际输出信号分别为U1=k1F1、U2=k2F2，通过试重法确定系数k1，k2。
在两个校正面已知的位置上分别放置两个已知质量的砝码，让其以某一确定的速度旋转，输出波形为U'1=k1F1、U'2=k2F2，根据输出的两个波形可以确定出两个幅值大小，可以看出幅值是关于不平衡量m1r1、m2r2、相位角φ1，φ2、系数k1、k2的函数，而相位角、径向积都是已知的，惟有系数k1、k2是未知的。两个输出波形可以确定两个方程，这样就可以方便地求出系数k1、k2，这样输出波形与转台安放传感器处所受的力之间的关系就可以确定了。
可以采用傅氏级数展开的方法提取基频振动分量的大小和相位。如果在一个周期里，对振动信号进行等间隔采样，则可得出序列的DFT的基频量，但由DFT所得到的幅值和相位并不是不平衡信号的幅值和相位，二者存在着确定的对应关系，可推导得出振动信号基频分量的振幅和初相。

3 结论
本文设计的动平衡测试系统采用立式旋转方法测不平衡量，解决了大型弹箭体积大、质量重用通常的卧式旋转无法实现的问题，适合测量大型重物动不平衡量。从力学角度具体的分析论述了不平衡量是以怎样的方式反映到输出波形上的，为动平衡测试软件的设计打下了基础。