标准孔板e值的间接测量方法
时间:11-25
来源:互联网
点击:
流量测量节流装置是差压式流量计的一个重要组成部分,一般包括节流件、取压装置和前后测量管等。节流件主要有孔板、喷嘴和文丘里管等。可以根据GB/T2624.2-2006/ISO5167-2:2003《用安装在圆形截面管道中的差压装置测量满管流体流量第二部分:孔板》提供的数据和要求进行设计、制造、安装和使用的节流件作为标准节流件,如标准孔板、标准喷嘴和标准文丘利管等。其中,各种型式的标准孔板的几何形状都是相似的,其轴向平面横截面如图1所示。
针对图1中的几何参数,根据GB/T2624.2-2006和JJG640-1994《差压式流量计》检定规程,基本都有明确的技术要求和检验方法,大部分也都可以较容易地测得。但根据GB/T2624.2-2006第5.1.6.1项:“若孔板的厚度E超过节流孔厚度e,孔板的下游侧应切成斜角,斜角表面应精加工”。此时,节流孔的上游侧端面与节流孔的轴线是垂直的,但下游侧的端面是一锥面,不与孔的轴线相垂直,这样一来,就无法使用常规计量器具直接测量e值。根据JJG640-1994第19.4条所述,检验e值所用主要仪器是工具显微镜(模压法)或e值测量仪。但据了解,e值测量仪没有合适成品供选择,而采用模压法进行测量时,在模压器的制作、安装以及模压操作时的位置和操作方法等方面都有较高的要求,一般情况下较难掌握。因此,本文主要介绍节流孔厚度e值的一种间接测量方法。
该方法的具体数学模型是:e=E-h·cotα,如图2所示。
式中:e——所要测的节流孔厚度值;E——节流孔板的厚度值;h——下游侧斜面的径向宽度;α——斜面的斜角。
二、测量方法不确定度的评定
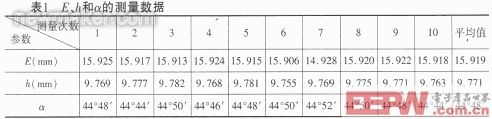
以上游管道内径D为508mm为例,根据相关要求,设计标准孔板E为(16.00±0.20)mm,e为(6.00±0.20)mm,α为45°±1°。分别对E、h和α进行10次测量,测得值如表1所示。
于是各分量的传播系数:
①E值测量重复性引入的标准不确定度分量uE1,由统计方法获得。
根据表1中的数据,由贝塞尔公式得:
根据JJG21-1995《外径千分尺》检定规程,壁厚千分尺示值误差为±4μm,设均匀分布,于是有 ?0.0023mm。
?0.0023mm。
(2)测量h值引入的标准不确定度分量uh
①h值测量重复性引入的标准不确定度分量uh1,由统计方法获得。
根据JJG56-2000《工具显微镜》检定规程,工具显微镜示值误差为(1+L/100)μm,当测量范围较小时,可认为引入的误差约等于1μm,设均匀分布,有 0.0006mm。
0.0006mm。
(3)测量α值引入的标准不确定度分量uα
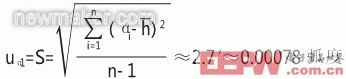
①测量重复性引入的标准不确定度分量uα1,由统计方法获得。
根据表1中的数据,由贝塞尔公式得:
根据JJG33-2002《万能角度尺》检定规程,万能角度尺示值误差为±2',设均匀分布,于是有
 各标准不确定度分量具体数据如表2所示。
各标准不确定度分量具体数据如表2所示。
三、结论
上述实例验证了该方法能较好地完成对节流件标准孔板e值的测量。
针对图1中的几何参数,根据GB/T2624.2-2006和JJG640-1994《差压式流量计》检定规程,基本都有明确的技术要求和检验方法,大部分也都可以较容易地测得。但根据GB/T2624.2-2006第5.1.6.1项:“若孔板的厚度E超过节流孔厚度e,孔板的下游侧应切成斜角,斜角表面应精加工”。此时,节流孔的上游侧端面与节流孔的轴线是垂直的,但下游侧的端面是一锥面,不与孔的轴线相垂直,这样一来,就无法使用常规计量器具直接测量e值。根据JJG640-1994第19.4条所述,检验e值所用主要仪器是工具显微镜(模压法)或e值测量仪。但据了解,e值测量仪没有合适成品供选择,而采用模压法进行测量时,在模压器的制作、安装以及模压操作时的位置和操作方法等方面都有较高的要求,一般情况下较难掌握。因此,本文主要介绍节流孔厚度e值的一种间接测量方法。
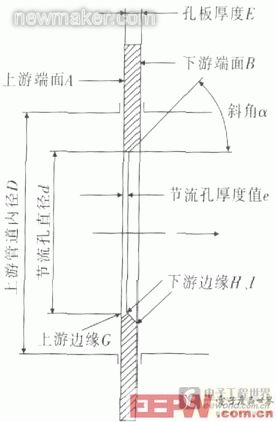
图1 标准孔板轴向平面横截面
该方法的具体数学模型是:e=E-h·cotα,如图2所示。
式中:e——所要测的节流孔厚度值;E——节流孔板的厚度值;h——下游侧斜面的径向宽度;α——斜面的斜角。
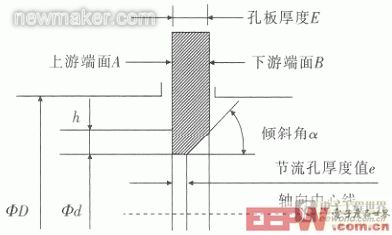
图2 数学模型原理
二、测量方法不确定度的评定
以上游管道内径D为508mm为例,根据相关要求,设计标准孔板E为(16.00±0.20)mm,e为(6.00±0.20)mm,α为45°±1°。分别对E、h和α进行10次测量,测得值如表1所示。
于是各分量的传播系数:
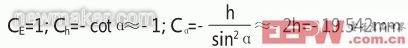
①E值测量重复性引入的标准不确定度分量uE1,由统计方法获得。
根据表1中的数据,由贝塞尔公式得:
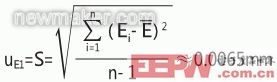
根据JJG21-1995《外径千分尺》检定规程,壁厚千分尺示值误差为±4μm,设均匀分布,于是有
 ?0.0023mm。
?0.0023mm。 (2)测量h值引入的标准不确定度分量uh
①h值测量重复性引入的标准不确定度分量uh1,由统计方法获得。
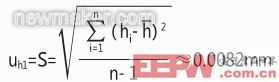
根据JJG56-2000《工具显微镜》检定规程,工具显微镜示值误差为(1+L/100)μm,当测量范围较小时,可认为引入的误差约等于1μm,设均匀分布,有
 0.0006mm。
0.0006mm。 (3)测量α值引入的标准不确定度分量uα
①测量重复性引入的标准不确定度分量uα1,由统计方法获得。
根据表1中的数据,由贝塞尔公式得:
根据JJG33-2002《万能角度尺》检定规程,万能角度尺示值误差为±2',设均匀分布,于是有

 各标准不确定度分量具体数据如表2所示。
各标准不确定度分量具体数据如表2所示。 表2 各标准不确定度分量数据 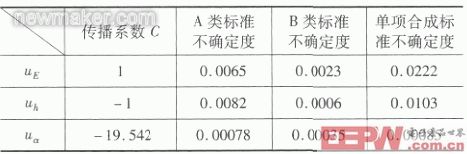

三、结论
上述实例验证了该方法能较好地完成对节流件标准孔板e值的测量。
- 平衡孔板流量计和标准孔板的比较(01-24)
- 测量天然气差压式流量计系统原理(01-21)
- 差压式流量计输出为零点的解决措施(01-21)
- 腐蚀性介质的流量测量(03-23)
- 孔板变形对流量测量的影响(03-23)
- 高温流体的流量测量(03-23)
