基于神经网络优化的油水界面软测量
原油脱水过程中油水界面的准确监测对油品的含水率、污水回收及处理成本都是极为关键的,能开发出在线的测量技术具有十分重要的现实意义。
遗传算法和神经网络都是将生物学原理应用于科学研究的仿生学理论成果,由于它们具有极强的解决问题的能力,近年来引起了众多科研人员和工程人员的兴趣和关注[1]。但神经网络和遗传算法作为传统的算法,不仅计算量大,消耗时间多,而且还需要专家进行校验[2-4]。因此,为了充分利用两种算法的优势,弥补两者之间的缺陷,本文采用了将两者结合的思想。
2 问题描述
在基于BP算法的多层前馈网络的应用中,以图1所示的单隐层网络的应用最为普遍。一般习惯将单隐层前馈网络称为三层前馈网或三层感知器,所谓的三层包括了输入层、隐层和输出层。隐层可以是单层,也可以是多层,前层至后层节点通过权连接。
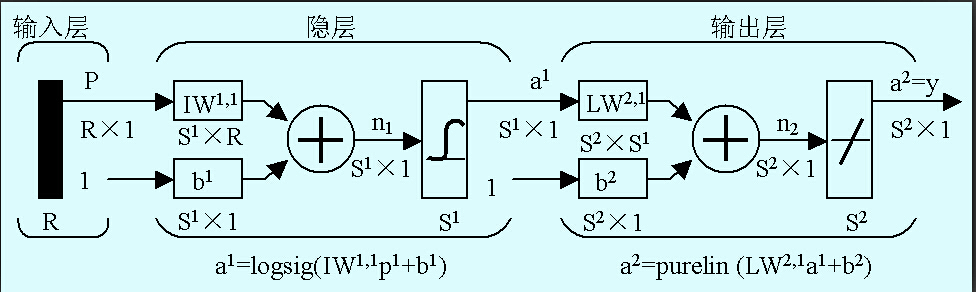
图1 BP网络结构
输入矢量维数为R,隐层神经元的个数为S1,输出层神经元的个数S2,a1表示隐层神经元的输出矢量,a2表示输出层神经元的输出矢量,W1,1表示隐层神经元域为任一集合。对适应度函数唯一的要求是输入可计算出能加以比较的非负结果。适应度函数具体的计算方法为:将染色体上表示的各个参数分配到BP网络的结构上,结合训练样本集的输入与输出,计算网络的输出后得到网络实际输出与希望输出的误差,取误差平方和作为目标函数,即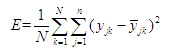 (3)
(3)
式中为网络输入输出样本对个数;为输出层节点个数;,为当输入第个样本时,第个输出节点的期望输出与实际输出。
遗传算法以适应度函数作为进化目标,且只能朝着适应度函数值增大的方向进化,所以适应度函数与目标函数之间要进行适当的转换。由于进化中的网络误差是非零正数,可将目标函数的倒数作为适应度函数,即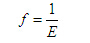 c) 遗传算子的选择。
c) 遗传算子的选择。
① 用轮盘赌法确定选择算子,种群中个体的选择概率为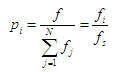 (5)
(5)
式中
为个体的适应度;
为种群的总适应度;
为个体的选择概率。
轮盘赌法的具体实现是:先计算出当前种群的总适应度,然后产生一个[0,1]之间的随机数,求取,并将满足下列条件的第个个体选中,进入交叉操作: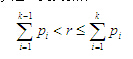 (6)
(6)
进行次这样的操作,得到个个体,与最优选择机制保留下来的适应度最大的个体,一起构成个个体,进入接下来的交叉和变异操作。
② 采用自适应的交叉概率的算法,使群体中最大适应度值的个体的交叉率和变异率不为零,分别得到提高,这就相应地提高了群体中表现优良的个体的交叉率和变异率,使得它们不会处于一种近似停滞不前的状态。
种群中个体的交叉概率为 (7)
(7)
其中为常数;为“早熟度”,用来评价种群是否早熟的指标,其计算公式为,其中表示种群中个体适应度的最大值,表示个体适应度大于整体平均适应度的个体的平均适应度。
在二进制编码中,采用的是单点或多点交叉。对于实数编码来说,采用这些方法是困难的,本文采用算数交叉,即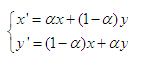 (8)
(8)
式中,为父代个体;,是子代个体;为(0,1)间的实数。
交叉时由于码串选取的是最大可能长度,不会产生混乱现象。
③ 采用自适应的变异概率的算法,使遗传算法具有局部的随机搜索能力,在接近最优解的邻域时加速向最优解收敛,维持种群多样性,防止出现不成熟收敛。
种群中个体的交叉概率为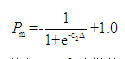 (9)
(9)
其中为常数。
非一致变异算子可以增强局部搜索能力,因此本文采用非一致变异操作进行算子的变异。假设为父代种群中的一个个体,其中。随机选取中的一个基因,假设为第个基因,进行变异,则子代个体为。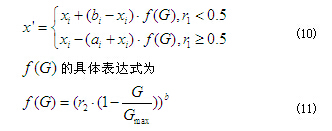
神经网络油水界面软测 相关文章:
- 频宽、取样速率及奈奎斯特定理(09-14)
- 为什么要进行信号调理?(09-30)
- IEEE802.16-2004 WiMAX物理层操作和测量(09-16)
- 为任意波形发生器增加价值(10-27)
- 基于PCI 总线的高速数据采集系统(09-30)
- 泰克全新VM6000视频测试仪助力数字电视等产品测试 (10-06)
