基于TMS320LF2407A DSP的PFC级电路的原理与设计

增益Ks和PFC输出直流总线电压感测增益Kd分别表示为：
Kf=1/Vmax
　　Ks=1/Imax
　　Kd=1/Vo(max)
　　式中，Vmax为整流的输入电压Vin最大允许幅值，V；Imax为输入电流Iin的最大允许幅值，A；Vo(max)为直流总线电压最大允许值，V。

3.2 输入电压前馈软件的实现

输入电压前馈能使输入功率保持在规定的电平上，不随AC线路电压波动而变化。

为计算输入电压Vin的平均成分Vdc，需要计算信号频率f（=1/t），然后对一个周期上的信号进行积分，如图3示图所描述。

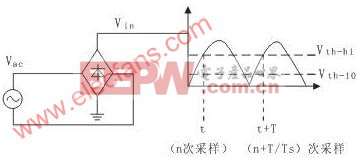
图3 和Vin平均成分的计算

3.2.1 频率计算

在频率软件执行期间和其后的平均Vin的计算，每当信号跨越上门限Uth-hi时，Vin的采样数（N）被计数并被保存。信号的下门限Uth-Io用于获得抗扰度。若采样周期为Ts，采样频率为fs=1/Ts。Vin的周期为T，N=T/Ts。若N为已知数，每单位（per unit, Pu）频率fpu的计算公式是：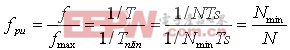

　　式中，fmax为Uin的最大频率，Hz；Nmin为Uin一个周期上的采样最小数。计算频率的用户软件利用N值，首先计算中间值1/N，然后与Nmin相乘得到fpu值。为保存1/N值，并带最高精度，不引起累加器溢出，知道Nmin值是很重要的。为此，用户应当选择信号最大频率以被测量。一旦知道Nmin值，1/N量可以被保存，并带最大精度且用适当的定点表示。例如，对于一个输入工作频率为47~63Hz的PFC变换器，最大输入频率可以选择70Hz。然后用fmax=140Hz（两倍的输入频率）和已知的Ts值来计算Nmin，是非常容易的。

3.2.2 前馈成分计算

只要知道信号Vin的频率，它的平均成分Vdc可用下面公式计算：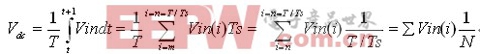

　　式中，T为相应于Uin频率f的时间周期， S；Vin（i）为Vin的数字化i次采样。

由于Vin作为相对于它的最大值Vmax的每单位（pu）规格化值被测量，所计算的Vdc值也是一个带Vmax规格化基本值的每单位（pu）量值。对于一个正弦波输入电压，Vac的最大值仅为2Vmax/π。因此，在Vac的固定点表示中，为获得最佳精度，先前计算的值相对于它自己的最大值被转换为每单位规格化量值，这个值由下式给出：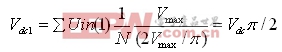

　　Vdc1的倒置电压Vinv（即Vinv=1/Vdc1）在Vdc1最小时值最大，反之亦然。为在Vinv固定点表示中获得较高的精度，需要用相对于其最大值的每单位（pu）规格化值来表示。对于一个正弦波输入电压，Vdc的最小值是2Vmin/π。输入电压最小幅值Vmin的选择，基于PFC变换器的输入电压范围。例如：若PFC变换器的低线路RMS电压是90V，Vmin值应低于或等于127V（ ）。Vinv的最大值为（Vminπ/2），相对于它自己最大值的相应Vinv的每单位（pu）值为：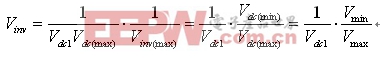

　　3.3 乘法器增益Km

乘法器增益Km的调节，应能在最低输入电压上，当PFC变换器交付最大负载时，使参考电流Iref是在它的最大值上。在图2中，Iref为

　　随电流环路闭合，Iref可表示为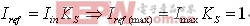

　　在最低工作电压Vinv=1时，满载下的电压控制器输出将在它的最大值上，即Vnv=1。因此，在最低工作电压上，为产生最大参考电流，要求Km值为：

　　3.4 电压和电流环路补偿器

电流环路功率级高频近似值为：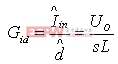

　　根据图2所示的PFC控制框图，电流环路增益等式为：

　　式中，Fm为调制器增益，

调制器在软件中部分地执行，并部分地利用DSP PWM硬件。软件利用调制器输入，即电流控制器输出Uca，计算在TMS320LF2407A中PWM硬件模块的占空比值。PWM硬件利用占空比值，为PFC开关产生适当的PWM信号。当调制器输入Uca是1时，软件保证调制器输出即PWM占空比为100%。在此情况下，调制器增益Fm=1。因此，对于电流环路的交越频率fci，需要的电流误差放大器补偿器可以表示为：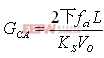

　　只要电流环路闭合，电压环路功率级传输函数可按下式计算：

　　式中，Zf为输出电容CO和负载阻抗ZO组成的并联分支的等效阻抗，Zf=ZO/（1+sCOZO）；负载阻抗 。

图2中电压环路增益等式如下：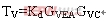

电压环路交越频率fcv需要的电压误差放大器补偿器为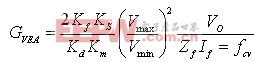

　　3.5 电压和电流环路补偿器软件的实现

先前给出的电压和电流环路控制器，在它们利用TMS320LF2407A在软件中被执行之前，被变换为如下说明的等效数字形式，电流控制器可以写为：

　　式中：KP为已计算的电流补偿器量值；E为电流误差信号。

电流环路补偿波德（Bode）曲线如图4所示。其中：顶部为电流环路控制单元增益Gid、Fm和KS曲线；中间为补偿器Gca增益曲线；底部为所期望的环路增益Ti曲线。功率级有一个-1的斜率，在期望的穿越频率fci上放置零点fz，可以产生一个45°的相补角。然而，由于控制环路采样和补偿延时，相补角的一部分被损失，因此将fz放置到图4所指示的位置，以补偿相补角损失。

图4 电流环路补偿波德曲线

4、PFC级数字控制器设计实例

在本