遗传模糊算法在短期负荷预测中的应用

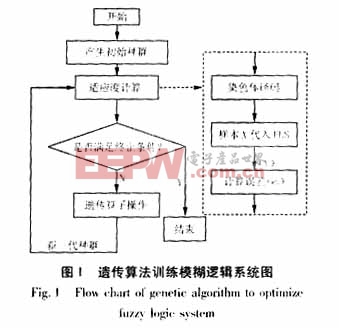
图1表示了基于遗传算法的模糊逻辑系统的训练过程。设种群规模为K，每一次迭代所产生的染色体为lj(j=1,2,...K)。在适应度计算模块中，首先对每次新产生得染色体lj进行解码，还原成其所确定的模糊逻辑系统Lj。然后将样本集合的输入
集合的输出量Y进行统计处理，抽取误差平方和作为分析指标，即染色体lj对应的统计量作为其目标函数，如式（1）：
　
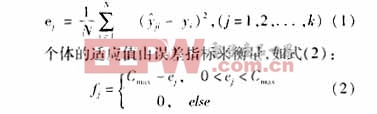
　　其中，Cmax为一给定值。选取f*为系统的最优适应值，当循环迭代出现期望的适应值fo(fo≥f*)时，迭代终止，由此确定最优模糊逻辑系统。

2 模糊负荷预测系统的参数选取
　　该系统的工作过程分为两个阶段：训练阶段和预测阶段。训练阶段是将已知的历史负荷资料作为评价指标，利用遗传算法对模糊逻辑系统的参数进行选择，这一阶段可以看作是一个对人类经验（备选解群）进行计算机总结进而寻找出最优模糊逻辑系统的过程。预测阶段即系统的实际应用阶段，将预测日的相关因素输入预测系统，得出预测结果。
　　 本文设计的模糊负荷预测系统共分为24个独立的小系统，每个小系统针对24个不同的时刻，对样本数据分区处理。而在对预测日负荷进行集中预测。

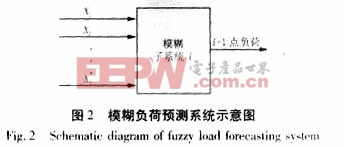
图2所示的结构为小系统i的输入输出关系。模糊关系用Mamdani最小规则定义，合成算法使用“∧－∨”运算准则，解模糊转换采用重心法（亦称为加权平均法）。输入变量X的选取一般考虑的因素为：日期类型、天气状况(气温、降雨量、湿度和风速等)、负荷近期变化趋势等一些因素。根据区域性和季节性对负荷变化影响的差异，不同的系统可以选取不同的输入量。通过研究预测地区的负荷特性在近几年的变化情况，本文选取输入量X有三(即图2中的n=3)：X1为周日期类型；X2为预测日时刻T的气温；X3为近期负荷变化趋势。具体的定义见2.1节。
2.1系统输入量及其隶属函数的选取
　　输入量X1为预测日的日期类型。根据负荷的周循环特性，模糊词集定义为T（A1）={周一，周二，周三，周四，周五，周六，周日}。显然，该词集中的各元素之间不存在模糊关系。为适应模糊逻辑系统运行，需要将其按照模糊数学形式处理，即定义

　　这一变量的隶属函数参数实际上已经确定，因此不参与随后的遗传算法的寻优过程。
　　输入量X2为预测日T时刻的气温预报。该变量为影响负荷预测的主要因素，且与负荷变化成非线性关系，按照隶属函数的选取原则[7]，将模糊词集划分为T(A2)={NB(负大),NS(负小),ZE(中),PS(正小),PB(正大)}，经过反复的试验，本文对上述的词集依次选取梯形(偏小型)，三角形、梯形（偏大型）三种形式。

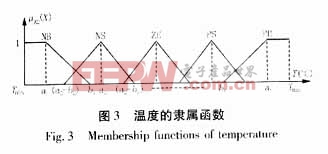
如图3所示，温度隶属函数中所需调节的参数为a1、b1、a2、b2、a3、b3、a4、b4、a5、b5等十个参数。每个参数对应的调节范围是[Umin，Umax]。值得注意的是，论域UT=[Tmin,Tmax]的选取可按照季节的不同进行设定，以期提高预测的精确度。
　　输入量X3为预测日前三周相应日0时刻负荷量的加权平均值。它反映了负荷的近期变化趋势。结合文献[6]中的平均值求法，给出如公式（4）:
　
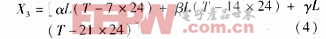
　　其中α＋β＋γ＝1，α≥β≥γ。该量代表过去3周同类型日同一时刻T的负荷的加权平均值。如果过去3周同类型日中的某一天正好是节日，则取再前一周的数据，并根据α、β、γ的调节确定近期与远期历史数据对当前的影响。这一输入中包含负荷的动态信息和近期的发展趋势，对于预测的准确性是至关重要的。
　　其隶属函数的确定方式与输入量X2相似，但因该变量与预测负荷基本成线性关系，因此选取的隶属函数个数较少，选定三个模糊词，即T(A3)={NB(低),ZE(中),PB(高)}。
　　同理，输出量Y分为4档，设定模糊词集T(B)={NB(负大),NS(负小),PS(正小) ,PB(正大)}。
2.2 推理规则的选取
　　 推理规则由一系列多维多重模糊条件语句组成，本文中输入量有三个，因此是三维多重模糊条件语句，其基本形式为“IFx1 is Ali and x2 is A2j and x3 is A3k THEN y=Bm”。其中i、j、k分别为各输入量的隶属函数个数，m为输出量隶属函数的个数。由此可知本文系统可能的规则数为7×3×5＝105个，对105个模糊条件语句的确定实际上是对每一条语句选择合适的Bm。

3 遗传算法应用中的问题
　　编码方式的优劣决定了遗传算法总体效果的优劣，它直接影响着遗传算法的搜索能力和保持种群稳定性。如果编码不适当，会使得不可行解过多，搜索可行解困难重重，往往需要加上大量的前期或后期补救措施才能够完成计算。因此，如何制定优良的编码策略是绝大部分遗传算法问题中的重要问题。对几种编码进行分析比较后，本系统选用二进制编码方式，每三位基因串表示隶属函数的一个参数；使用两位基因表示每条推理条件句的推理结果，然后将两个基因串连接起来，形成表征模糊逻辑系统的染色体。
　　对于表示隶属函数的基因串部分，假设某一参数ai(或者bi)的取值范围是[Umin，Umax]，用一l位数来表示，其关系表示如下： u=Umin+(n/(2t-1))(Umax-Umin)。本文中l=3。正如第二节中所述，该系统输入量X2有5个隶属函数，输入量X3共有3隶属函数，输出量Y为4个隶属函数，每个隶属函数的待定参数为两个，于是基因串共长72位，形如下式：