交流调感稳压电源中等效电感的分析
)三种计算等效电感方程式之间的关系是: 式(14)表示的是Le与控制角α之间的关系,使用比较方便,故应用较普遍,式(5)在介绍稳压原理时使用方便,这两公式形式不同但实质是一样的。式(15)是不正确的,但可以用,在应用时必须要除2才能得到正确值。 3高频PWM斩波器调感电路Le的计算 图4用高频PWM斩波器调感的等效电路 图5EPWM调制与正弦PWM斩波波形 i=1,2,3…(16) 输出电压偏差ΔU为采样电压,触发脉冲起点ti和终点ti+1的方程式为: 由于PWM斩波波形是镜对称和原点对称,因此它的付里叶级数中将只包含正弦项中的奇次谐波,即: 经计算,当n=KN±1时(K=1,2,3…) 当n≠KN±1时,bn≠KN±1=0 对于基波,n=1 =MUm(19) uLe=MUmsinωt sin(KN±1)ωt(20) 如求等效电感Le,由图4 表1基波和各次谐波幅值与Um之比(fc=10kHz,N=200) ![]() 高频PWM斩波器调感的等效电路如图4所示,斩波开关用IGBT和一个单相整流桥组成,由于工作于高频,所以采用了软开通和软关断缓冲电路,以减小IGBT的开关损耗。开关控制采用了EPWM直流等电位调制技术。触发脉冲的形成与交流电压PWM斩波波形如图5所示。为使波形半波奇对称和四分之一偶对称,以消除付里叶级数中的余弦项和偶次谐波,使载波比N==4K,K=1,2,3…,fc
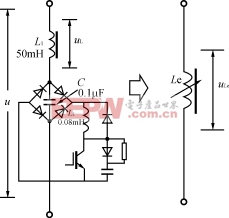
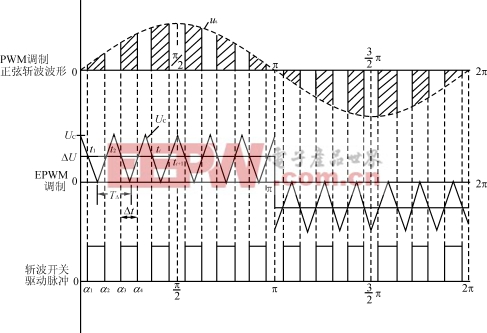
高频PWM斩波器调感的等效电路如图4所示,斩波开关用IGBT和一个单相整流桥组成,由于工作于高频,所以采用了软开通和软关断缓冲电路,以减小IGBT的开关损耗。开关控制采用了EPWM直流等电位调制技术。触发脉冲的形成与交流电压PWM斩波波形如图5所示。为使波形半波奇对称和四分之一偶对称,以消除付里叶级数中的余弦项和偶次谐波,使载波比N==4K,K=1,2,3…,fc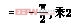
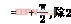


![]()
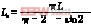
![]()
![]() 为三角波频率,fs为市电工频;调制M=,Δt为脉冲宽度,TΔ=为三角波周期、Uc为三角波幅值、ΔU为输出电压的偏差、三角波电压的方程式为:
为三角波频率,fs为市电工频;调制M=,Δt为脉冲宽度,TΔ=为三角波周期、Uc为三角波幅值、ΔU为输出电压的偏差、三角波电压的方程式为: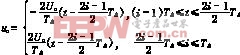
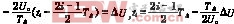
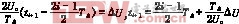
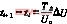 脉冲宽度Δt=
脉冲宽度Δt=![]() 式中TΔ=,各触发脉冲的起点角和终点角的数值为:
式中TΔ=,各触发脉冲的起点角和终点角的数值为: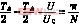
![]() α1=(1-M);α2=(1+M)
α1=(1-M);α2=(1+M)![]()
![]() α3=(3-M);α4=(3+M)
α3=(3-M);α4=(3+M) ![]() uL=bnsinnωtn为奇数
uL=bnsinnωtn为奇数![]()
![]() bn=uLsinnωtd(ωt)=sinωt·sinnωtd(ωt)
bn=uLsinnωtd(ωt)=sinωt·sinnωtd(ωt)![]() +sinωt·sinnωtd(ωt)+…)(17)
+sinωt·sinnωtd(ωt)+…)(17) 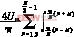 bn=KN±1=sinωt·sinnωtd(ωt)
bn=KN±1=sinωt·sinnωtd(ωt) =-(18)
=-(18) ![]()
![]() b1=sin2ωtd(ωt)+sin2ωtd(ωt)+…)
b1=sin2ωtd(ωt)+sin2ωtd(ωt)+…)
![]()
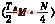 =sin2ωtd(ωt)=
=sin2ωtd(ωt)= ![]()
![]() -sinKMπ·
-sinKMπ· ![]() 由式(18)的谐波幅值sinKMπ可以算出:当fc=10kHz,N=200,M=0.1~0.9时,基波和各次谐波幅值与Um之比如表1所示,它们和调制比M的关系曲线如图6所示。可知,N越大谐波频率越高。当fc=50kHz,N=1000时用电路中L1=50mH,C=0.1μF就可以滤掉uLe中的所有高次谐波。
由式(18)的谐波幅值sinKMπ可以算出:当fc=10kHz,N=200,M=0.1~0.9时,基波和各次谐波幅值与Um之比如表1所示,它们和调制比M的关系曲线如图6所示。可知,N越大谐波频率越高。当fc=50kHz,N=1000时用电路中L1=50mH,C=0.1μF就可以滤掉uLe中的所有高次谐波。 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 b1/Um 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 b199/Um -0.0984 -0.1871 -0.2575 -0.3027 -0.3183 -0.3027 -0.2575 -0.1871 -0.0984 b201/Um -0.0984 -0.1871 -0.2575 -0.3027 -0.3183 -0.3027 -0.2575 -0.1871 -0.0984 b399/Um -0.0935 -0.1514 -0.1514 -0.0935 0 0.0935 0.1514 0.1514 0.0935 b401/Um -0.0935 -0.1514 -0.1514 -0.0935 0 0.0935 0.1514 0.1514 0.0935 b599/Um -0.0858 -0.1009 -0.0328 0.0624 0.1061 0.0624 -0.0328 -0.1009 -0.0858 b601/Um -0.0858 -0.1009 -0.0328 0.0624 0.1061 0.0624 -0.0328 -0.1009 -0.0858 b799/Um -0.0757 -0.0468 0.0468 0.0757 0 -0.0757 -0.0468 0.0468 0.0757 b801/Um -0.0757 -0.0468 0.0468 0.0757 0 -0.0757 -0.0468 0.0468 0.0757
M
谐波分量
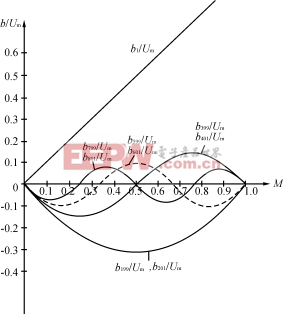
图6谐波分量与调制比M的关系曲线
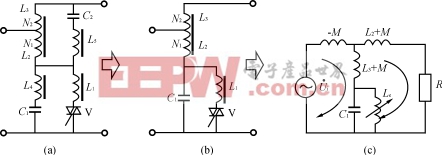
图7稳压电源主电路及其等效电路
(a)主电路(b)简化电路(c)等效电路
可知需使uL=uLe,uL=ULmsinωt,对于uLe忽略掉其中的高次谐波时(高次谐波被L、C滤掉)uLe=MUm·sinωt,当uL、uLe用有效值表示时:UL=MULe,两边各除以电流iL的有效值IL,则可得:![]() ωL1=MωLe,Le=(21)
ωL1=MωLe,Le=(21)
4稳压电源的输出电压方程式
交流净化电源和晶闸管调感式交流稳压电源的主电路和等效电路如图7所示,其中L1、L4、L5为线性电感。L4、C1组成三次谐波滤波电路,L5、C2组成五次谐波滤波电路,双向晶闸管V和L1组成调感支路,图7(a)为主电路,图7(b)为简化电路,图7(c)为等效电路。
对图7(c)用基尔霍夫定律可得到如下方程:![]()
![]() =〔-jωM+jω(L2+M)+jωLX〕-
=〔-jωM+jω(L2+M)+jωLX〕-![]() 〔jω(L2+M)+jωLX〕
〔jω(L2+M)+jωLX〕![]()
![]() =〔jω(L2+M)+jωLX〕-
=〔jω(L2+M)+jωLX〕-![]() 〔jω(L3+M)+jω(L2+M)+jωLX〕
〔jω(L3+M)+jω(L2+M)+jωLX〕![]() 两式联立对求解得:
两式联立对求解得:![]()
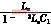
![]()
![]() 式中M=;LX=;=R
式中M=;LX=;=R
由式(22),在已知L1、L2、L3、C1、R和uo的条件下,当输入电压ui发生变化时,通过调节LX(实际上就是调节等效电感Le)就可以使输出
- 电源设计小贴士 1:为您的电源选择正确的工作频率(12-25)
- 用于电压或电流调节的新调节器架构(07-19)
- 超低静态电流电源管理IC延长便携应用工作时间(04-14)
- 电源设计小贴士 2:驾驭噪声电源(01-01)
- 负载点降压稳压器及其稳定性检查方法(07-19)
- 电源设计小贴士 3:阻尼输入滤波器(第一部分)(01-16)
