DC/DC变换器中输出滤波器的比较
对于恒频PWM变换器而言,最常用的控制参量是占空比D;对于谐振类变换器而言,最常用的控制参量是频率f。为便于对以上5类电压波形谐波的幅值进行比较,我们对D和f这2个控制参量进行了归一化处理,用λ来统一表示。在前3类电压波形对应的变换器中,λ=D;对于第4类电压波形,λ等于归一化的开关频率(f/2fr),其中fr为等效正弦半波的谐振频率;对于第5类电压波形,λ等于归一化的开关频率(f/fr)。从而归一化参量λ从0到1变化。 3滤波器大小的比较 3.1谐波含量的量度—K(λ) 首先,定义K(λ)为各电压波形首次非零谐波的幅值与其直流分量的比值。从而可以根据这一归一化 (a)半波整流 (b)全波整流 (c)第3类 (b)第2类 (a)第1类 (e)第5类 (d)第4类 DC/DC变换器中输出滤波器的比较 的函数K(λ)来对各种变换器拓扑中滤波元件的体积进行比较。表1给出了各类电压波形的平均值、1次谐波、2次谐波表达式及谐波的一般表达式。 从表1中,可以得到5类整流级电压波形所对应的K(λ)分别如式(1)~式(5)所示。K1(λ)=(1)K2(λ)=(2)K3(λ)=·(3)K4(λ)=(4)K5(λ)=(5) 上述5类电压波形K(λ)与λ的对应关系曲线如图3所示。K(λ)=0表示该工作点处,谐波幅值为零。 对于第1类波形(正激类),当λ=1时,整流级电压波形为直流; 对于第2和第3类波形,当λ=0.5时,整流级电压波形为直流; 对于第4类波形,当λ=1时,K4(λ)达到最低值。此时,图2(d)的正弦半波电压波形将占满整个周期,电压波形与第五类波形相似; 对于第5类波形,在整个频率变化范围内,K5(λ)恒等于2/3。 通过K1(λ)与K4(λ)的比较可见,在整流级电压的直流分量和导通时间相同的情况下,PWM变换器产生的方波比谐振变换器产生的正弦半波更容易滤波。 由上分析可知,K(λ)值越低,所需的滤波元件L、C值越小。因此,从滤波器大小的角度考虑,变换器应当尽可能设计工作在较低的K(λ)值下。但K(λ)往往受到电路拓扑的限制,不能达到理论分析的最低值。常见的如在正激变换器中,因为要折衷考虑变压器铁心去磁和功率管的电压应力,因此占空比不能取得太高,从而限制了K4(λ)的取小。 3.2滤波元件大小的比较—LC(λ) 在比较滤波器电抗元件大小时,必须注意两个重要的参量: 1)整流级电压波形的首次非零谐波的幅值〔用 K(λ)表示〕; 2)该非零谐波的频率。 对于一个LC输出滤波器,可以从以上两个方面出发,来提高其转折频率,从而减小滤波元件L、C的取值大小。具体描述如下: 1)如果能够降低整流级电压波形的首次非零谐波的幅值,则可以在保证相同输出电压纹波的情况下,适当提高滤波器在谐波频率处的增益,也即滤波器的转折频率得以适当提高(如图4,从A点移动到B点); 2)如果能够提高首次非零谐波的频率(如图4,从A点移动到C点),滤波器转折频率也得以提高,从而只需较小的滤波元件。 如在第2类和第5类电压波形中,所要滤除的首次非零谐波,其频率是开关频率的两倍,因而这两类拓扑中滤波元件LC的乘积可以减小为其它类电压波形对应取值的1/4。 表1电压波形的直流分量、谐波含量与控制参量λ的关系 第1类第2类第3类第4类第5类 2Upλ sin(λπ) Upλ 2Upλ sin(2λπ) sin(nλπ) sin(2λπ) sin(nλπ)(1+cosnπ) ·sin(λπ) ·sin(2λπ) ·sin(nλπ) · · · · 图4理想LC滤波器的波特图 为了对图2中各种电压波形在获得相同输出电压纹波时,所用输出滤波器的体积进行比较直观的比较,考虑首次非零谐波的幅值和频率,对滤波参数LC乘积进行了归一化处理。分别如式(6)~式(10)所示。其对应的关系示于图5中。LC1(λ)=(6)LC2(λ)=(7)LC3(λ)=·(8)LC4(λ)=(9)LC5(λ)=(10) 从以上分析,可以直观地看到: 1)第1类正激式变换器中Dmax一般不超过0.5,而且受开关损耗等因素的制约,开关频率不能取得太高,因此滤波元件LC的取值不能太小。 2)第2类在这类变换器中,整流级电压的频率是开关频率的2倍。而且,在移相控制全桥等典型变换器中,很容易实现软开
图2整流级电压波形
图1整流方式
图35类电压波形K(λ)与λ的关系曲线
平均值
一次谐波00
二次谐波
总表达式
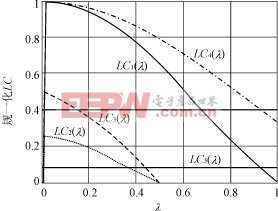
图5归一化的LC滤波器参数
- 电源设计小贴士 2:驾驭噪声电源(01-01)
- 适合高效能模拟应用的线性电压稳压器(07-19)
- DC-DC变换器中一种高性能振荡电路的设计(04-08)
- 弥补模拟控制器缺点的数字控制器(08-04)
- 欠压/过压锁定(08-25)
- 多重转换:冗余电源系统电流限制的一种新方法(12-24)
