较低次谐波的目的。这种槽口的安排如图4所示。图中决定槽口的开关角不再用参考信号和载波信号相互比较的方法来确定,而是利用输出电压波形的数学模型通过计算求得。对于图4所示的波形,考虑对称性,谐波成分中不含直流分量及偶次谐波。其傅立叶奇数表达式可以写成
uUn(t)=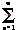 Bnsinnωt(n=1,3,5…) (8)
Bnsinnωt(n=1,3,5…) (8)
各次谐波的幅值为
Bn=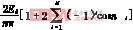 (9)
(9)
输出电压表达式为
uUn(t)=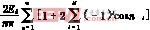 sinnωt (10)
sinnωt (10)
式中:αi就是需要确定的开关角。
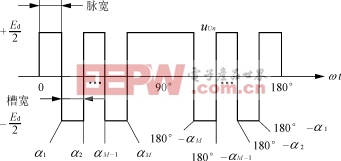
图 4 谐 波 消 去 法 的 槽 口 示 意 图
为了考查各次谐波的幅值,在此我们可以定义它们的相对值,令
An= (11)
(11)
式中:B10=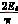 。
。
由式(11)可知,通过合理安排M个开关角,就可以消除M-1种谐波并控制基波电压。
通过以上的分析可知,谐波消去法是一种根据输出电压的数学模型直接确定开关角α的方法,其实质是一种优化PWM方法。这种方法的优点就是利用有限个开关角就能有效地抑制某些低次谐波。当然,它的缺点也很明显,计算复杂,要求消除的谐波越多,计算量也就越大。另外,通过这种方法只能使特定次数的谐波被消除,而其余次数的谐波却不能被消除,而且可能还会使之增大。但随着M的增大,未消去的谐波的次数也越来越高,这时谐波对电动机的影响已经不大了。在实际应用中,常常是先离线计算出α值,利用查表法快速而准确地实时确定开关角地值。
2.3 载波相移SPWM(CPS-SPWM)[4]
由于大功率器件的开关频率较低,而高的开关频率又会导致较大的开关损耗,降低系统效率,这使普通SPWM技术的应用受到了限制,而组合变流器相移SPWM技术能较好地解决了这一问题。该技术的基本思想是:在变流器单元数为Lx的电压型SPWM组合装置中,各变流器单元采用共同的调制波信号sm,其频率为km。各变流器单元的三角载波频率为kc,将各三角载波的相位相互错开三角载波周期的1/Lx,如图5(a)所示(变流器单元数Lx=5,SPWM频率调制比kc/km=3,幅度调制比ma=0.8)。图5(b)所示的Lx个波形分别为Lx个变流器单元的输出,上述Lx个变流器单元交流输出叠加形成整个组合变流器装置的输出波形,如图5(c)所示。对输出进行频谱分析,变流器单元之一的输出波形频谱如图5(d)所示,叠加后整个组合变流器输出波形频谱如图5(e)所示。比较图5(d)和图5(e)可见各变流器单元输出叠加后形成的组合变流器总输出波形中谐波得到了有效的抑制。
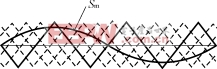
(a) 相 位 相 互 错 开 的 各 三 角 载 波

(b) Lx个 变 流 器 单 元 的 输 出 波 形

(c) Lx个 变 流 器 单 元 输 出 叠 加 波 形

(d) 一 个 变 流 器 单 元 输 出 频 谱

(e) Lx个 变 流 器 单 元 叠 加 组 合 输 出 频 谱
图 5 CPS-SPWM原 理 图
该技术的实质是多重化和PWM技术的有机结合,能够在低开关频率下实现大功率变流器SPWM技术,而且显著地减少了输出谐波,改善了输出波形,从而减少了滤波器的容量[5][6]。同时,如图6及图7所示,相移SPWM变流器具有良好的动态响应和较高的传输频带,使得许多先进的控制手段得以应用,控制性能得以提高。

(a) Nm=7,k=3组 合 相 移SPWM逆 变 器

(b) Nm=1,k=21单 个SPWM逆 变 器
图6 传 输 线 性 度 分 析
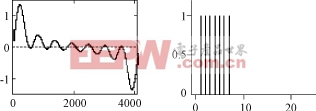
(a) 输 入 波 形 (b) 输 入 波 形 频 谱
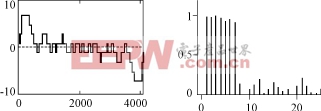
(c) 输 出 波 形 (d)输 出 波 形 频 谱
图7 传 输 带 宽 分 析
3 相移SPWM的数学分析
设有Lx个SPWM变流器单元,其中,第L个变流器单元输出的傅立叶级数展开为
FL(t)=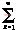 CLKcos(Kωt+φLK) (12)
CLKcos(Kωt+φLK) (12)
三角载波初始相位为
φLc=φc+(2πL/Lx) (13)
各个变流器单元有相同的调制波信号,其幅值和相位分别为
QLkm=Qkm
φLkm=φkm (14)
将Lx个变流器单元的输出波形叠加后,总的输出为
FT(t)=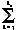 FL(t)=
FL(t)=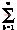
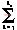 CLkcos(kωt+φLk) (15)
CLkcos(kωt+φLk) (15)
进一步推导,可推出相移SPWM组合变流器的输出频域表达式。其傅立叶级数的因子除下列各频率外均为零。
3.1 输出信号
当k=km时
CTk=Lx Qkm (16)
Qkm (16)
φTk=φkm
3.2 载波谐波
当k=MLxkc(M=1,2,…∞时)
CTk= Jo(MLxQkm)sin
Jo(MLxQkm)sin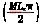 (17)
(17)
φLk=MLxφc
3.3 边带谐波
当k=MLxkc+nkm(M=1,2,…∞,n=±1,±2,…±∞时),
CTk=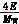 Jn(MLxQkm)sin(MLx+n)
Jn(MLxQkm)sin(MLx+n)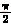
φTk=MLxφc+nφkm (18)
4 结语
在采样法SPWM中,对称规则采样方法简单,但变频器的输出电压比较低;而非对称规则采样法在一个载波周期里采样两次正弦波数值,使采样值更真实地反映了实际的正弦波数值,其输出电压较高。但由于采样次数增加,增大