新型EPWM斩波器式交流稳压电源的原理分析
采用图2所示主电路对市电电压波动进行补偿的关键有两点:一是EPWM;二是电容Cd的值要小到不影响整流电压ucd的变化,即使Cd小到不再具有直流滤波功能。
2 EPWM调制及正弦斩波电压的生成
图1所示交流稳压电路的EPWM,与正弦斩波电压的生成如图3所示。其中图3(a)为整流器VD1~VD4的交流输入电压波形,图3(b)为直流电容Cd上的电压波形,图3(c)为EPWM,图3(d)为EPWM产生的桥式斩波器中开关管V1~V4的触发脉冲波形,图3(e)即为EPWM正弦斩波电压波形,图3(f)为Tr初级补偿电压波形。
EPWM是由P.D.Parkh,S.R.Paradla于1983年首先提出来的。其原理是采用用直流形式表示的误差电压ΔU与三角波电压uc进行比较如图3(c)所示,在直流误差电压ΔU大于三角波电压的部分产生出等脉宽调制脉冲,如图3(d)所示。用图3(d)的等脉宽调制脉冲去触发桥式斩波器中相应的开关管V1~V4,就可以在桥式斩波器的两桥臂中点a和b之间产生出EPWM正弦斩波电压波形,如图3(e)所示。经过滤波器LFCF滤波后,就可以在变压器Tr初级得到正弦补偿电压uab1,如图3(f)所示。uab1在Tr次级产生补偿电压uco。当对市电电压进行正补偿时,补偿电压uco与市电电压相位相同;当对市电电压进行负补偿时,补偿电压uco与市电电压相位相反。图3是针对正补偿情况画出来的,对负补偿也可以画出相应的波形图。
对于图3(e)所示的EPWM正弦斩波电压波形,为了使此波形具有半波奇对称,和四分之一波偶对称,以消除其傅里叶级数中的余弦项和正弦项中的偶次谐波,使载波比N=fc/f=4k,即三角波频率fc为市电频率f的4整数倍。调制比M=Δt/TΔ=ΔU/Ucm,Δt为脉冲宽度,TΔ=1/fc为三角波周期、Ucm为三角波幅值,如图3(e)所示。可知,M=Δt/TΔ就是EPWM正弦斩波电压波形的占空比D,即M=Δt/TΔ=D。

(a) 整流输入电压
(b) 电容Cd上电压
(c) EPWM
(d) 斩波开关驱动脉冲
(e) EPWM正弦斩波波形
(f) 补偿电压
图3 EPWM斩波器式交流稳压电源的工作波形图
载波三角波的方程式为
uc=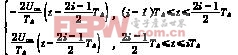 i=1,2,3,…(1)
i=1,2,3,…(1)
当调制电平为ΔU时,可求出触发脉冲起始点ti和终止点ti+1的方程式。
由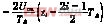 =ΔU,得到
=ΔU,得到
ti=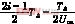 ΔU(2)
ΔU(2)
由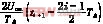 =ΔU,得到
=ΔU,得到
ti+1=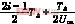 ΔU(3)
ΔU(3)
则脉冲宽度为
Δt=ti+1-ti=![]() ΔU(4)
ΔU(4)
式中:TΔ=2π/N。
各触发脉冲的起始角和终止角的数值为
α1=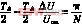 (1-D);α2=
(1-D);α2=![]() (1+D);α3=
(1+D);α3=![]() (3-D);α4=
(3-D);α4=![]() (3+D);
(3+D);
……
由图3(e)可以看出,EPWM正弦斩波电压波形是镜对称和原点对称,因此,在它的傅里叶级数中将不包含余弦项和正弦项中的偶次谐波,只包含正弦项中的奇次谐波,即
f(ωt)=![]() bnsinnωt n为奇数(5)
bnsinnωt n为奇数(5)
式中:bn=![]() f(ωt)sinnωtd(ω t)
f(ωt)sinnωtd(ω t)
对于基波,n=1。由于被EPWM斩波的波形是正弦波,即f(ω t)=Umsinωt,所以
b1=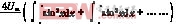 =
= =
=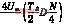 =DUm(6)
=DUm(6)
对于谐波,则
bn=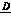
当n=kN±1,k=1,2,3,……时,对上式求解得
bkN±1=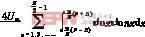 =-
=-![]() sinkDπ(7)
sinkDπ(7)
当n≠kN±1时,bn≠kN±1=0。
所以EPWM正弦斩波电压的傅里叶级数表示式为
uab=DUmsinωt-![]() sinkDπsin(kN±1)ωt(8)
sinkDπsin(kN±1)ωt(8)
考虑到Tr的变比ξ:1,补偿电压uco表示式为
uco=D![]() sinωt-
sinωt-![]() sinkDπsin(kN±1)ωt(9)
sinkDπsin(kN±1)ωt(9)
用LFCF滤除高次谐波后得到补偿电压为
uco=D![]() sinω t=D
sinω t=D![]() (10)
(10)
由式(8)中的谐波幅值![]() sinkDπ可以算出,当载波三角波频率fc=10kHz,N=200,D=0.1~0.9时,基波与各次谐波的幅值如表1所列。基波和各次谐波与调制比亦即占空比D的关系曲线如图4所示。可知EPWM正弦斩波电压的谐波频率与载波比N成正比,N越大谐波频率越高,所需的滤波器LFCF的参数值也越小。所以,根据表1及图4可以计算LF及CF的值。
sinkDπ可以算出,当载波三角波频率fc=10kHz,N=200,D=0.1~0.9时,基波与各次谐波的幅值如表1所列。基波和各次谐波与调制比亦即占空比D的关系曲线如图4所示。可知EPWM正弦斩波电压的谐波频率与载波比N成正比,N越大谐波频率越高,所需的滤波器LFCF的参数值也越小。所以,根据表1及图4可以计算LF及CF的值。
表1 基波与各次谐波的幅值(fc=10kHz,N=200)
| 谐波 分量 | 占空比D | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
| b1/Um | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| b199/Um | -0.0984 | -0.1871 | -0.2575 | -0.3027 | -0.3183 | -0.3027 | -0.2575 | -0.1871 | -0.0984 |
| b201/Um | -0.0984 | -0.1871 | -0.2575 | -0.3027 | -0.3183 | -0.3027 | -0.2575 | -0.1871 | -0.0984 |
| b399/Um | -0.0935 | -0.1514 | -0.1514 | -0.0935 | 0 | 0.0935 | 0.1514 | 0.1514 | 0.0935 |
| b401/Um | -0.0935 | -0.1514 | -0.1514 | -0.0935 | 0 | 0.0935 | 0.1514 | 0.1514 | 0.0935 |
| b599/Um | -0.0858 | -0.1009 | -0.0328 | 0.0624 | 0.1061 | 0.0624 | -0.0328 | -0.1009 | -0.0858 |
- 简述数字电位器基本原理与基本特性(12-09)
- 工程师福利:倾情奉献无线充电器设计原理及BOM清单(12-09)
- 集中器侧硬件原理图设计(12-09)
- 开关电源原理与设计主要器件之开关电源变压器(12-09)
- 变频器工作原理及控制方式介绍(12-08)
- 小型UPS电源的原理与维护(12-08)
