业界广泛使用的LLC原理与设计

电流迅速减小到励磁电流。在谐振电流减小到励磁电流前，变压器副边仍有电流流动，变压器原边仍被箝位，因此谐振电流的下降斜率为（Vc-n.Vo)/Lr, Vc为谐振电容上的电压。副边整流二极管D2上的电流逐渐减小，当协整电流等于励磁电流的时候，D2的电流减小到0，实现ZCS.

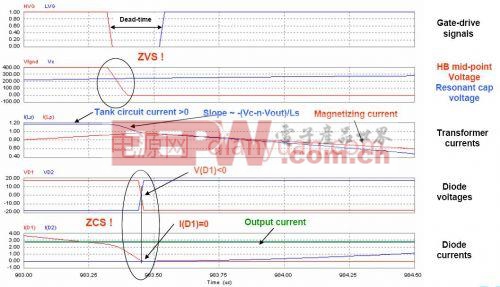
在t1时刻前，Q1两端的电压为零，励磁电流通过Q1的体二极管流通。此时使Q1开通，Q1便是ZVS。Q1导通后，Ls,Cr开始另一半周的谐振。副边二极管D1导通。

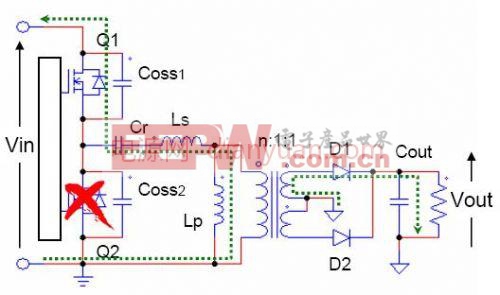
在t2时刻，谐振电流反向。直至t3时刻Q1关断，开始另一半周的工作，其工作过程与t0-t3相同。

由上面的分析和波形可以看出，当fs>fR1时，LLC原边实现ZVS，副边实现ZCS，副边二极管工作在电流断续的状态。

我们再来看一下当fR2fsfR1时候的情况。当fR2fsfR1时，开关周期长于谐振周期，原边激磁电感将参与工作。这种工作状态，也正是LLC与传统的串联谐振电路的区别所在。

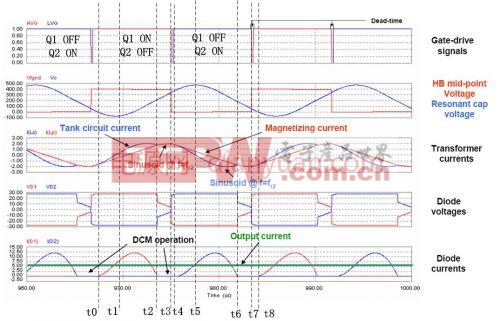
在t0时刻，上管Q1导通，下管关断。Ls与Cr谐振，谐振电流反向流过Q1，副边二极管D1导通，向负载提供能量。变压器原边被输出箝位，励磁电流线性增大。

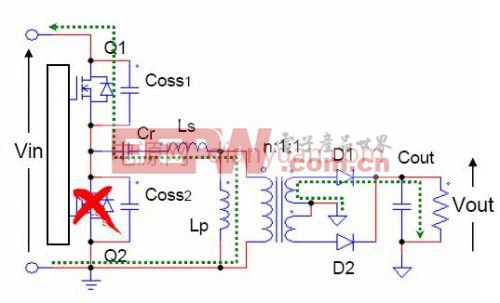
在t1时刻，谐振电流反向，正向通过Q1。

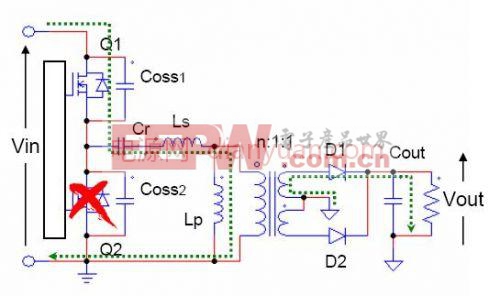
由于fsfR1,开关周期长于谐振周期。因此到t2时刻，谐振电流与谐振电流相等。副边二极管电流降为0，自然关断。此后，Ls,Cr与原边激磁电感Lp构成谐振，由于谐振频率很低，t2-t3的时间远小于开关周期，因此电流近似为线性变化。

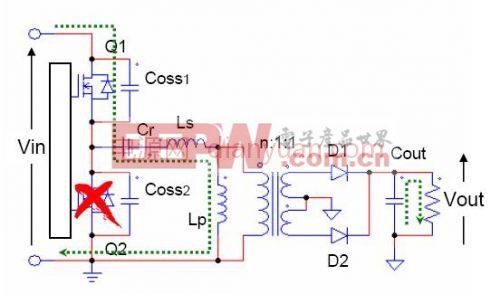
在t3时刻，Q1关断。原边电流向Coss2充电，使下管Q2能实现零电压开通。

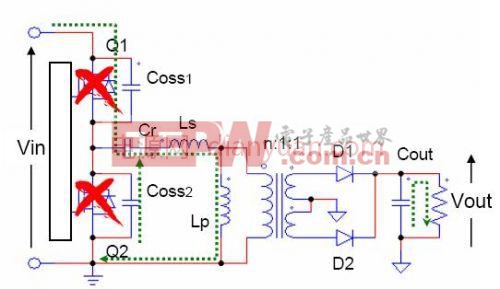
t4时刻，Q2导通，开始另一半周的工作。其过程与t0-t4相同。

对于LLC的参数设计，主要是确定：1，所希望的特性，轻载和满载的特性，取决于K和Q；2，工作点，开关频率是高于谐振频率还是低于谐振频率，主要取决于变压器的匝比；3，确定参数，漏感和励磁电感的大小，谐振电容的容值。

从前面的分析我们可以看到，LLC变换器最关键的LLC谐振槽路的设计。对于半桥网络，只提供一个频率可变，50%占空比的方波激励。对于理想变压器和输出整流网络，其增益是固定不变的。因此为了更好的研究LLC谐振槽路的特性及设计，我们需要简化LLC谐振槽路的输入输出模型。对于谐振槽路，起主导作用的是激励的基波成分。因此我们用基波等效（FHA)来等效输入模型。

上面是一个LLC的电路，我们可以等效为如下的等效电路。

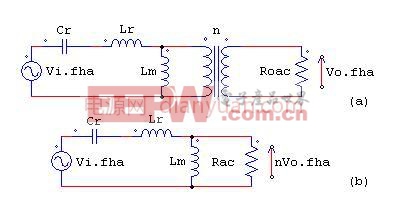
对于谐振槽路的输入端，也就是Q1,Q2连接点，我们通常称为半桥中点，其电压波形为一个幅值为Vdc的方波，

经过傅里叶分解，我们可以得到它的基波为：

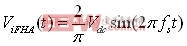
其有效值为

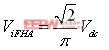
由于变压器副边绕组的电流为正弦波，对于全桥整流电路，

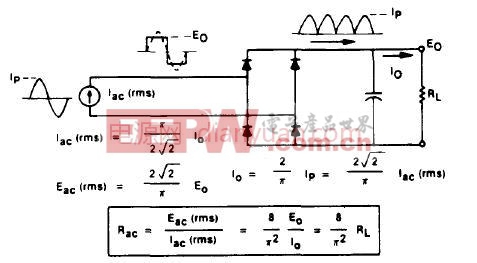
此分析同样适用于全波整流，因此

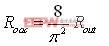
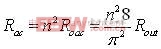
得到输入输出的等效后，我们可以计算谐振槽路的增益。

从归一化的增益公式，我们可以看到，影响LLC增益的因素有fn,k,Q. 对于fn,通常我们希望它稳态时为1。所以我们先来讨论下k的影响。我们可以改变k的数值，得到不同的Q值曲线图。

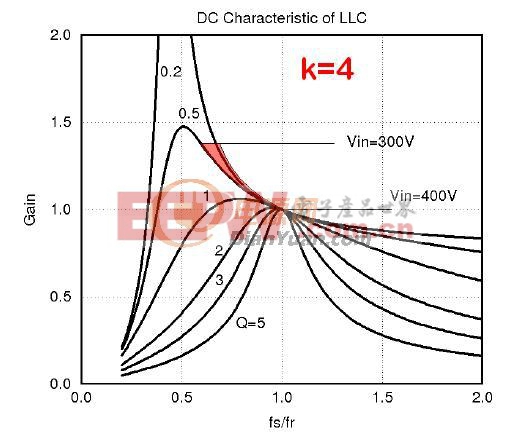
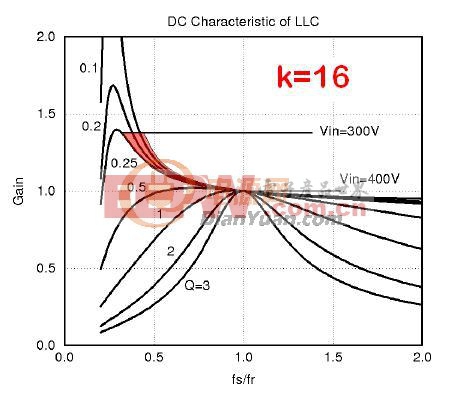
从上面不同的Q值曲线上，我们可以看到，k值越小，Q值曲线越陡峭，要获取相同增益时，频率变化越小。

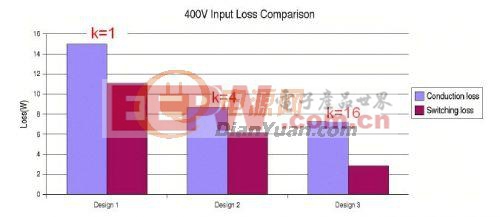
那么K值是不是越小越好呢？答案是K值并不是越小越好。K值越小，意味着相对于相同的Lr, 励磁电感Lm要越小，开关管的损耗会增大。所以通常情况下，我们把K值取在3-7之间。

当我们确定K值后，就可以得到一组Q值曲线。我们如何去理解这个Q值曲线呢？当我们的输入和输出电压固定的时候，并且变压器变比固定的时候，根据上面的公式，我们是可以得到一个固定的我们所需要的谐振槽路的增益M。当对应于某一个输入电压时，我们需要谐振槽路提供的增益为Mx.我们可以在Q值曲线上画一条Mx的直线，Mx这条直线和Q值曲线相交的点，就是LLC在不同负载下的工作点。

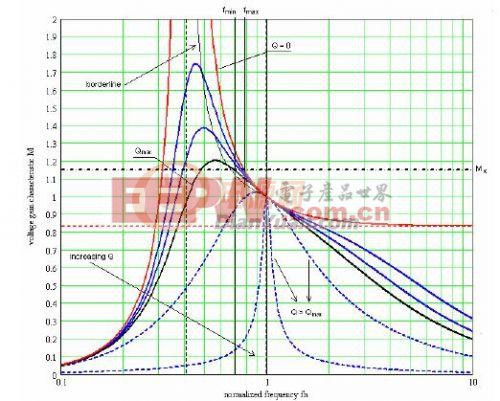
从图上我们可以看到，当负载增大时，Q值也增大，Q值曲线左移，Q值曲线与Mx相交点的频率是降低的。因此我们可以看到当负载增加的时候，LLC的工作频率是减小的。从物理意义上来讲，当负载阻抗Rac减小的时候，Lr与Cr构成的串联谐振回路上的阻抗也要减小，以维持Rac上得到的分压不变。只有通过降低频率才能使Lr和Cr构成的串联阻抗减小。因此，当负载加重时，LLC的开关频率是减小的；当负载减轻的时候，LLC的开关频率是增大的。

从上面的分析我们可以看到，当输入输出电压，负载以及变压器变比确定的时候，LLC的开关频率就确定了，也就是LLC的工作点是确定的了。那么我们如何去调整这个工作点呢？

从上面的分析可以看出，LLC的工作点与增益有关。当谐振参数确定后，唯一能改变增益的就是变压器的变比。因此要改变LLC的开关频率，只有通过改变变压器的匝比来实现。

对于LLC，还有一个很重要的参数就是Q值。我们来看一下