蓄电池剩余容量预测技术现状及发展

看[31][32][33][34]，主要将内阻(电导)法应用于蓄电池失效预警，直接应用于SOC预测的很少(一般作为SOC影响因素之一与电压法、神经网络等方法结合使用)[36]。且文献[30]经过大量实验得出结论：单体电池的电导值为参考值的80%以上时，蓄电池正常，且容量在80%以上；当电导值为参考值的60%—80%时，其容量很可能不足80%，蓄电池处于“普通危险”状态，需要做全放电测试；当电导值为参考值的60%以下时，蓄电池处于“严重危险”状态，需要及时更换。

3系统辨识及参数估计模型方法预测SOC

2000年左右，系统辨识及参数估计模型方法开始被应用于蓄电池SOC估计，目前在国内外研究中比较热门。它主要是应用一些新的方法(主要是人工智能算法)对蓄电池进行系统建模，将影响SOC的各种因素综合到电池模型中，通过大量试验对模型进行系统辨识和参数估计，得到蓄电池某些参数与SOC之间的关系，进而估算SOC。比较常用的人工神经网络法、向量机法、模糊推理法以及卡尔曼滤波法等。

3.1神经网络法

由于蓄电池是一个复杂的非线性系统，对其充放电过程建立准确的数学模型难度较大。而神经网络具有分布并行处理、非线性映射和自适应学习等特性，可较好地反映非线性的基本特性，在有外部激励时能给出相应的输出，因此能够在一定程度上模拟蓄电池动态特性，估算SOC[36][37]。

估算蓄电池SOC大多采用典型的3层人工神经网络[38][39]。一般直接采集蓄电池的放电电流、端电压以及温度或采用变电流组合测量方法，确定电动势和内阻作为神经网络模型的输入，SOC作为输出。其中输入、输出层神经元一般为线性函数；隐含层节点数目取决于问题的复杂程度及分析精度，可根据网络在训练过程中的收敛速度和训练完成后的误差来确定。人工神经网络法适用于各种蓄电池，但该方法的误差受训练数据和训练方法影响很大，而且实际使用中存在噪声干扰影响网络的学习与应用。从目前的文献来看，神经网络主要是理论方面研究。

文献[40][41]将另一种神经网络——支持向量机(SVM)方法用于蓄电池SOC估计，避免了传统神经网络在训练时间、局部最优以及收敛速度方面存在的缺陷。而文献[42]则进一步提出利用相关向量机(RVM)对蓄电池SOC进行预测，比支持向量机预测精度更高，预测模型也更加稀疏，不过算法也更加复杂，需要占用较大的计算机资源。

3.2模糊逻辑法

模糊逻辑法是对蓄电池进行模糊建模，以系统的输入、输出测试数据为依据，不受先验知识，经验与行为所限制。该方法通常对作为模型的输入变量的参数(如电压、电流、温度、内阻等)进行模糊化处理，根据大量的蓄电池特性试验数据得到SOC与电流、电压、温度等因素之间的关系，设计模糊规则并进行模糊推理，经反模糊化处理估计电池SOC[43][44][45]。

模糊逻辑方法的主要缺点是需要大量的实验数据，根据实验数据获得模糊推理规则和经验公式。目前该方法主要应用于仿真和理论分析，尚未应用于实际。

3.3卡尔曼滤波法

卡尔曼滤波理论的核心思想，是对动力系统的状态作出最小方差意义上的最优估计，它既适用于线性系统也适用于非线性系统[46]。

在运用卡尔曼滤波法估算SOC时，首先要建立适合于卡尔曼滤波估计的电池模型，且模型须具备两方面特点：(1)能够较好地体现电池的动态特性，同时阶数不能太高，以减少处理器的运算量，便于工程实现；(2)模型必须能够准确反映电池电动势与端电压的关系，从而使闭环估计有较高的精度。常用的等效电路模型有Randle模型(见图1)、MassimoCeraolo模型、Thevenin模型、Shepherd模型等，其中各个参数都为待定参数，需要根据实验数据计算得到[47][48]。

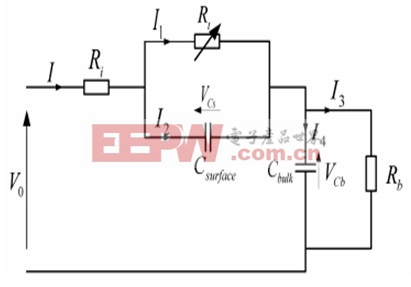
图1Randles电池模型

在实际应用中，卡尔曼滤波法通常与开路电压法以及安时法结合使用。其基本过程为：将模型中电容上的电压作为系统的状态，经卡尔曼估算出该电压后，利用模型中的数学关系求出电池电动势（或开路电压），最后由电动势与SOC的关系求出SOC。电池模型的卡尔曼数学形式为：

状态方程：

(9)

观测方程：

(10)

安时法方程：

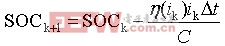(11)

系统的输入向量uk中，通常包含蓄电池电流、温度、剩余容量和内阻等变量，系统的输出yk通常为蓄电池的工作电压，蓄电池SOC包含在系统的状态量xk中，Ak、Bk由试验得到的参数确定，ωk、vk为系统噪声。估计SOC算法的核心，是建立一套包括SOC估计值和反映估计误差的、协方差矩阵的递归方程，协方差矩阵用来给出估计误差范围。方程(11)是电池模型状态方程，将SOC描述为状态矢量的依据。

卡尔曼滤波在估算过程中能保持很好的精度，并且对初始化