基于C++的电力潮流计算牛-拉法与P-Q法的分析比较

矩阵生成模块：根据网络拓扑结构计算出导纳矩阵;

(2)节点功率误差模块：根据功率误差公式计算出各节点功率误差;

(3)雅可比矩阵生成模块：由NR法修正方程式系数矩阵公式计算出雅可比矩阵;

(4)修正方程式求解模块：解修正方程式得到修正量;

(5)节点电压修正模块：用修正量去修正各节点电压值。

流程图见图1。

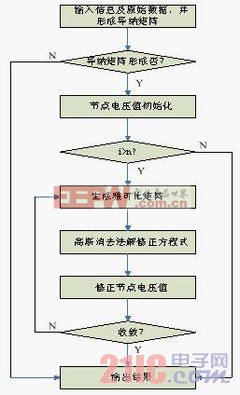
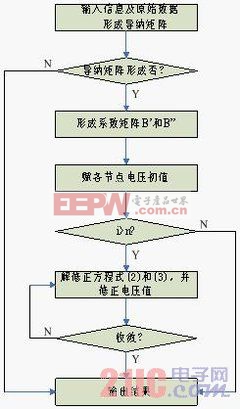
图1 NR算法模块化函数编程及流程图 图2 PQ算法模块化函数编程及流程图

3.3 PQ算法模块化函数编程及流程图

(1)导纳矩阵生成模块：根据网络拓扑结构计算出导纳矩阵;

(2)根据功率误差公式计算出各节点功率误差的模块;

(3)生成修正方程系数矩阵的模块;

(4)高斯消去法解 修正方程式的模块;

(5)高斯消去法解Q-V修正方程式的模块;

(6)修正各节点电压值的模块。

流程图见图2。

3.4 算法编程细节问题说明

初始电压用“平启动”方式，即e=1.0,f=0.0给出;用高斯消去法解修正方程式;NR法雅可比矩阵的形成与迭代同步进行，即每次迭代时系数矩阵都将不同。对高压电力系统，雅可比矩阵中各行的最大元素是有功功率误差量对电压的横分量e的偏导数与无功功率误差量对电压的纵分量f的偏导数，它们都不在对角元素位置。为减少计算过程舍入误差，程序通过对调雅可比矩阵中奇数行和偶数行的位置来实现最大元素放在对角元素位置上，以提高计算精度;对PQ分解法将BX法应用于程序编写。修正方程式的系数矩阵在每次迭代计算时都将固定不变，在电网拓扑结构数学模型的建立之初就已确定，与每次电压相量迭代结果无直接关系;由于Vector只能对一维向量进行存储，而矩阵相当于一个二维数组，就出现了如何将二维数组转化成一维向量的问题。对于一个i行j列的二维数组，可通过下面语句将其转变为一维向量：

vector Matrix;

for(i=0;i MatrixSize;i++)

for(j=0;j MatrixSize;j++)

Matrix[i* MatrixSize+j]=X[i][j];

其中，一维向量的大小即MatrixSize*MatrixSize，它等于二维数组X[i][j]中所有元素的个数(也就是矩阵的大小)。由此解决矩阵存储的问题;收敛条件可根据需要输入，当满足收敛性要求时计算结束。

4. 基于C++的两种不同算法的实验验证

图3 包含5节点的网络模型算例 图4 敛代特性对数坐标比较

以图3的网络模型为算例，以 为收敛条件。用C++编程，使用NR算法的输出结果(直角坐标系)如表1，使用PQ算法程序的输出结果(极坐标系)如表2。

表1：NR算法程序的输出结果

表2：PQ算法程序的输出结果

表3：两种算法比较

由表1和表2的比较可以看出，无论NR法还是PQ法得到的计算结果一致。另外使用IEEE14和IEEE30的算例继续用这两种算法程序计算，汇总结果可得到如下结论(如表3)：

对于相同的收敛条件，PQ法比NR法计算时所需要的迭代次数随着复杂度的增加而增加，相应的运行时间也较长;但对于迭代一次所需的时间，PQ法要比NR法少很多。另外对于不同的收敛条件继续使用NR算法程序和PQ算法程序计算，根据试验数据可绘制敛代特性比较图大致如图4所示，以A点为界，在A点之左，PQ法比NR法收敛的快，而在A点之右，NR法比PQ法收敛的快。

5.结论

综上可见，偏重于满足数据精度要求时，可采用NR算法来计算网络潮流的分布情况，而偏重于满足计算速度要求时应当选择PQ法，这就是PQ法也应用于电力网络潮流在线计算