Newton-Raphson迭代法

摘要：在非线性电子电路的静态分析之中，提出了一种数值计算方法——Newton-Raphson迭代法。该方法是在建立起电子电路的结点电压方程之后，应用Newton-Raphson迭代，从而可获得电路结点的直流电压。这种分析方法具有计算简单、准确等特点。
关键词：电子电路；静态分析；Newton-Raphson迭代法

在电子电路的分析中，静态分析(又称直流分析)是电路分析的基础。然而，众所周知，电子元器件是非线性的，因此，电子电路的分析实际上就是非线性电路分析。
非线性电子电路的静态分析有多种方法，如图解法、模型法、分段线性法及估算法等。图解法是分析非线性电路的有效方法之一，但是图解法的作图过程比较烦琐，计算精度差，当非线性元件较多时则无法作图。模型法是在一定的条件下忽略了非线性元器件部分影响相对较小的次要因素，而得到的便于认识和分析的简化了的理想化的模型。分析计算的精确度则取决于模型的精度。模型越复杂，计算越准确。采用模型法对学习和研究有一定的简化作用，但每种模型有限定的运用条件和运用的范围。分段线性法通过把非线性特性作分段线性化近似处理来分析非线性电路的一种方法。在分段线性化处理后，所研究的非线性电路在每一个区段上被近似等效为线性电路，就可采用线性电路的理论和方法来进行分析。但分段线性法要用到深奥的非线性电路理论。估算法是电子电路静态分析常常采用的方法，为了快速获得清晰的、定性的概念和结论，在一定的条件下，只考虑影响计算结果的主要因素，而忽略其次要因素。比如文献在分析二极管电路时认为，二极管的导通压降可近似取为0．7 V(硅管)或0．2 V(锗管)等。利用估算法可以大大地简化电子电路的静态分析，然而要能正确使用估算法也不是很容易的。因为有些问题的简化处理往往是一定条件下的经验数据，或者是前人经过严格的计算或实验证明而得出的结论。在我们没有搞清应用条件时，一味的使用估算法，有时会得出我们自己都不敢相信的结论。
本文将Newton-Raphson法应用到了非线性电子电路的静态分析之中。这种方法根据电路理论，首先列写出电子电路的结点电压方程，然后应用Newton-Raphson法，对非线性电路方程进行数值计算，计算结果就是电子电路的静态工作点值。概念简单，求解方法有效、精确。

1 电子电路的静态分析
根据电路理论，写出电子电路结点电压方程为

其中，ε是根据计算精度要求给定的常数。

2 算例
例1：

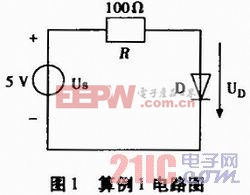
在图1所示电路中，设二极管伏安特性为：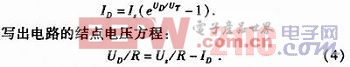


取UT=26 mV，ε=10-6，当Is=10-12A、10-10A、10-8A、10-6A、10-4 A时，二极管管压降UD分别为0．636 974 V、0．517 940 V、0．398 887 V、0．279 817 V、0．160 784 V。可见，在不同的Is下，UD与估算值0．7 V或0．2 V相差较大。
例2：

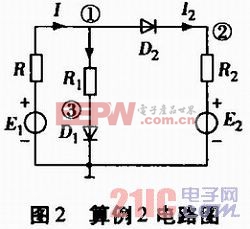
对于图2所示电路，设R=10 Ω，R1=R2=100 Ω，E1=12 V，E2=5 V，Is1=Is2=10-10A，UT≈26 mV。写出电路结点电压方程：

根据(2)、(3)式得出(7)式的迭代格式为：


3 结论
应用Newton-Raphson迭代法于电子电路的静态分析之中，可以有效地求出电子电路的静态工作点值，计算简单，数据准确，是一种有效的非线性电子电路静态分析方法。