便携式功率分析仪设计----硬件设计（一）

波功率成正比，以此来测定功率。这些使用热效应法的功率计因为其受温度影响很大，所以结构和测试技术复杂，对环境温度和测试设备要求苛刻。

以上这些功率计是热效应功率计，诺加热敏电阻、镇流电阻和热偶等热效应微波传感器，它们的热学时间常数较大。当被测信号是周期性脉冲时，这些功率传感器通常跟不上脉冲包络的变化，因而不能显示脉冲峰值功率。在稳定状态下，这种热效应功率计的读数，只能表示该射频脉冲在重复周期内的平均功率，由此可见并不能满足射频微波方向的应用。迄今，其响应速度能真实地跟上脉冲调制，并用于峰值电平测量的功率传感器，是晶体二极管(用于低功率测量)和真空二极管(用于高功率测量)。通常用于测量峰值脉冲功率的经典方法主要是：平均功率法和峰值检波功率测量法。

然而平均功率法主要的缺点在于，平均功率法是利用响应缓慢的功率传感器测量射频脉冲峰值功率的一种方法。该方法是测量重复脉冲的平均功率，并采用某种辅助方法来测量脉冲的占空系数。用连续波功率探头按照一般连续波功率测量的方法进行测量，得到平均功率测量结果后按照ASK调制的占空比进行计算，得出发射信号的脉冲功率。

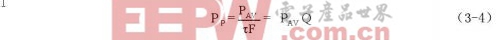
其中，PAV为平均功率测量结果，Q=1/τF是射频脉冲的占空系数(工作周期)，—般为10-2～10-4。当脉冲波形为非理想矩形脉冲时，必须对波形失真进行修正，其峰值脉冲功率的表达式为：

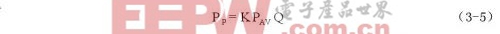
式中，K是波形修正系数，其数值等于实际脉冲功率的最大电平(峰值功率电平)与具有同样宽度和面积的等效矩形脉冲电平之比。K值经常是加以估计的，理想矩形脉冲的K=1.平均功率法的优点是，适应于较宽的频率范围，具有较大的功率量程;缺点是不适用于可变占空系数的场合，必须精确测量脉冲参量以及测量的间较长。而在实际应用过程中这种方法得到的结果中难免带有占空比测量和计算带来的误差，不能满足射频脉冲信号功率分析的要求。

所以通过分析，峰值检波功率测量法由于是对被测信号进行检波，然后根据用户指定的触发电平并延迟指定的时间在检波包络上进行采样得到测量结果，该方法测量可信度高，并且有测量效率高，对测量环境要求较低等特点，符合便携式功率分析仪的设计理念。故在本课题设中被采纳。

3.1.2功率测量方案

利用峰值检波器可直按测量脉冲功率。这种方法是测量检波器输出端的信号电压，该电压与加到检波器上的脉冲功率成比例。则我们只需要测得该时刻检波器输出电压值，即可求出该点被测信号功率大小。

通常，采用真空二极管作峰值检波器，其频率范围可达2～2.5GHz;晶体二极管(低势垒肖特基二极管)用作峰值检波器，频率范围可达18GHz.工作在平方律状态的晶体二极管，其动态范围约为20 dB.对于线性区域工作的真空二极管，动态范围从零点几瓦到200瓦，若采用外部分压器，上限可提高到几百千瓦，测量误差为(10～15)%。在精确测量射频功率时对检波器温度稳定性要求很高。而且由于半导体的温度特性影响，二极管检波器的温度稳定性较差，不能适应室外复杂外界条件下的测量需要。在低输入功率下，二极管探测器处于限制动态范围(20到30dB)，漂移也比较大。当系统需要检测控制RF功率时，解调对数放大器是一个越来越受欢迎的选择。

所以在实际设计过程中，采用对数放大器对功率调制信号进行检波。商业现有的对数放大器IC的优点是，与二极管检测器相比，动态范围提高4倍，温度稳定更好、更小。像二极管检测器一样，对数放大器基本上是电压敏感器件，而不是功率敏感器件。

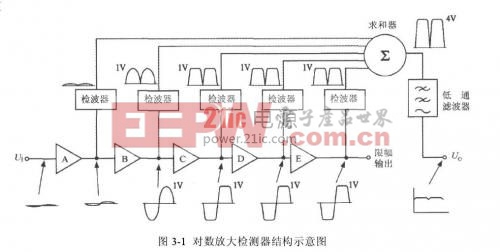
对数放大检测器是由多级对数放大器构成的，其电路框图如图3-1所示。图中共有5个对数放大器(A～E)，每个对数放大器的增益为20dB(即电压放大系数为10倍)，最大输出电压被限制为1V.因此，对数放大器的斜率k s =1V/20dB=50mV/dB.5个对数放大器的输出电压分别经过检波器送至求和器(∑)，再经过低通滤波器获得输出电压U o。对数放大器能对输入交流信号的包络进行对数运算，其输出电压与b、PIN的关系式为：

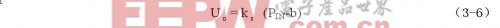
上式中的b代表截距，即对应于输出电压为零时的输入功率电平值。对数放大器的特性曲线如下图所示。由图可见，对应于±1dB的测量误差，输入功率电平的动态范围是-65dB～-5 dB.对数放大检测法的优点是动态范围宽，斜率恒定，并且温度稳定性好。

3.2功率测量部分方案设计

功率测量通道主要实现射频脉冲峰值功率实时测量。功率测试的设计思路：衰减-检波-放大-A/D采样。

功率测量电路主要包括微波部件、峰值检波电路、A/D转换电路和FIFO存储电路等。输入信号通过控制信号切换到功率测量通道后，根据信号的范围，控