模式匹配算法在入侵检测中的应用

足上述两种情况的s的最小值作为移动距离。因此可以定义一个距离函数distl(j)：

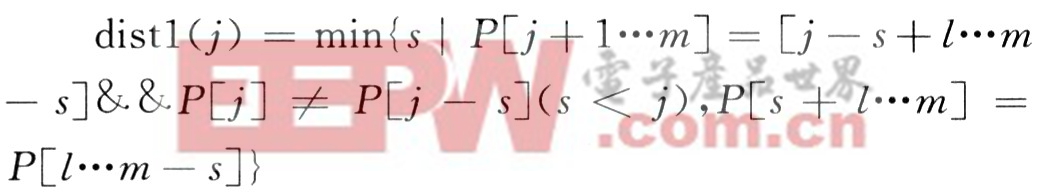
(2)坏字符移动。P中的某个字符与T中的某个字符不相同时使用坏字符移动。右滑距离函数dist2(x)定义如下：

匹配时取移动距离为：dist=max{distl(j)，dist2}。文献证明算法需要的预处理时间为O(m+σ)，最坏运行时间为O[(n―m+1)m+σ]，即扫描部分运行时间为O[(n―m)m]。在大字母表(相对于模式长度)情况下，BM算法非常快，实际比较次数只有目标串长度的20％～30％。
1．4 RK算法
Karp和Rabin在1981年提出来的RK算法利用了Hash方法和素数理论。
RK算法的思想是：首先定义一个Hash函数，用该函数计算出模式串P的Hash函数值，再计算出目标串T中所有长度为m的子串的Hash函数值，然后用相应的Hash函数值进行比较。当出现Hash冲突时，再进行相应字符串的比较，当构造Hash函数的素数选择得合理，Hash冲突出现的概率就可以做到很小。
Hash函数的构造及相应Hash值的计算如下：

设c∈∑，构造Hash函数：
h(asc(c))=asc(c)mod q
式中：q∈[1…n2m]且为素数；asc(c)为任意字符c的ASCII码。
映射模式串P为Hash函数值x(0≤x≤q一1)的方法为：
令：

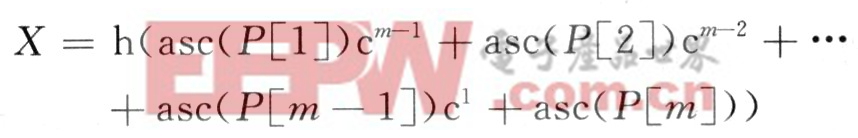
同理，映射目标串T中长度为m的子串t1=T[i…i+m一1]为Hash函数值ti的方法是：
令：

根据上述公式可把目标串T中每个长度为m的子串的Hash函数值计算出来。
如果Hash冲突不发生，即不再需要额外的字符匹配，RK算法的时间复杂度是O(m+n)；若考虑字符匹配，则RK算法的时间复杂度是0(mn)。在实际应用中，可设法取适当大的素数q，使得mod q仍可执行并且Hash冲突又几乎不发生，从而使得KR算法的实际运行时间只需O(m+n)。
RK算法采用了与KMP和BF算法不同的思路，尽量减少字符之间的比较次数，从而达到提高效率的目的。
1．5 单模式匹配算法改进情况简介
研究人员对单模式匹配算法提出了不少变形和改进算法。
在文献中黄占友等人提出的KMP算法的改进对特殊的字符串能够提高效率；文献中庞善臣等人对BM算法的改进有效地减少了最坏情况下的比较次数，同时方便在二位匹配和不精确匹配中推广；文献中贺龙涛等人通过将好后缀与坏字符两种情况合并进行处理对BM进行改进。采用该思想的同类改进算法还有很多，如：发表于2006年12月32卷23期《计算机工程》上渠瑜等人的对《对BM模式匹配算法的一个改进》，限于篇幅，不一一列举。在文献中张国平等人对BM算法的改进是通过定义一个距离函数来求出每次匹配失败时的最大可能移动距离；文献蔡晓妍等人对BM算法的改进则是结合了BM算法和TunedBM算法的优点，采用TunedBM的坏字符和BM的好后缀对模式进行预处理，然后根据当前尝试中匹配失败字符的位置信息，决定查找好后缀跳跃表还是坏字符跳跃表以期获得更大的跳跃距离。文献张立航等人对RK算法的改进是通过引入2次Hash运算进行的。通过两次Hash运算使出现Hash冲突的情况大为减少。

2 多模式匹配算法
2．1 入侵检测中采用多模式匹配的必要性
与单模式匹配算法相比，多模式匹配算法的优势在于一趟遍历可以对多个模式进行匹配，从而大大提高了匹配效率。对于单模式匹配算法，如果要匹配多个模式，那么有几个模式就需要几趟遍历。当然多模式匹配算法也适用于单模式的情况。在入侵检测系统中，一条入侵特征可能匹配或部分匹配很多条规则，如果采用单模式匹配，在匹配每条规则时都需要重新运行匹配算法，效率很低。然而，日益增多的网络攻击使得入侵检测的规则数目仍在不断增长，例如，Snort1．8．3的规则为1 270条，snort2．O的规则为2 300多条，到Snort 2．6．1则增加到3 600多条规则，因此，单纯提高单模式匹配算法的效率，很难使入侵检测系统满足越来越大的网络数据吞吐量和日益增加的攻击。
目前比较常见的多模式匹配算法有Aho―Corasick算法、Aho―COrasick―Boyer-Moore算法、Manber―Wu算法、Set一Wise Boyel-Moore一Hospool算法等。下面介绍其中2种经典的多模式匹配算法。
2．2 AC算法
AC算法1975年产生于贝尔实验室，最早用于图书馆的书目查询程序中。该算法基于有限状态自动机(FSA)，在进行匹配之前先对模式串集合SP进行预处理，形成模式树(树形FSA)，然后只需对目标串T扫描一次就可以找出所有与其匹配的模式串P。模式树K的构成如下：
K的每一条边e上都用1个字符作为标签；
与同一节点相连的边的标签均不同；
每1个模式p∈SP都存在1个节点v，使得L(v)=p，其中L(v)表示从根节点到口所经过的所有边上的标签的拼接；
每一个叶子节点v，都存在一个模式p∈SP使得以L(v’)=p。
例如：对于模式集SP={he，she，his，hers}模式树如图3所示，其中圆圈表示节点，双圈是根节点，边上的字符就是该边的标签，填充点圈的标签就是各个模式。