DNLMS滤波器的FPGA实现

0引 言

自适应滤波器一直是信号处理领域的研究热点之一，经过多年的发展，已经被广泛应用于数字通信、回声消除、图像处理等领域。自适应滤波算法的研究始于20世纪50年代末，Widrow和Hoff等人最早提出最小均方算法(LMS)。算法由于结构简单，计算量小，易于实时处理，因此在噪声抵消，谱线增强，系统识别等方面得到了广泛的应用。为了克服定步长LMS算法中收敛速度、收敛精度及跟踪速度等对步长大小选取相互矛盾的缺点，人们提出了许多变步长LMS算法，但是，当输入信号具有强相关性时，例如语音信号，LMS算法及NLMS算法的收敛速度将急剧下降。因此，本文对进入自适应滤波器的输入信号首先进行解相关预处理，再对自适应滤波器进行归一化LMS。

很多自适应滤波器是在通用DSP处理器上通过编写软件代码实现。这种滤波器在系统实时性要求不高的情况下，能很好地满足滤波要求，但在实时性要求较高的场合(如3G移动通信，网络会议等)，这种滤波器在处理速度和抗干扰性能等方面已不能满足要求。而用FPGA硬件实现的数字滤波器就能很好的解决并行性和速度问题，而且其具有灵活的可配置特性和优良的抗干扰能力，因而自适应滤波器的FPGA实现成为近年来数字滤波器中研究的热点。Altera公司开发的DSP Builder可以完成FPGA的DSP系统设计，它结合Matlab／Simulink提供的库元件和强大的计算仿真能力，进行图形建模和仿真，还可以完成从Simulink模块文件向VHDL语言的自动转换。

1 算法概述

在标准LMS算法中，其迭代公式如下：



式中：ω(n)为自适应滤波器在时刻n的权矢量；x(n)为时刻n的输入信号矢量；d(n)为参考信号；e(n)是误差信号；μ是步长迭代因子，为了增加LMS算法的收敛速度，文献[1-4]提出了不同的变步长算法代替定步长因子μ，但是很多变步长因子的计算量大，存在开方和指数运算，故在能满足要求的情况下，归一化LMS (NLMS)依然是一个很好的选择，即用μ_n／[x^T(n)x(n)]代替定步长因子μ为了控制失调，在更新公式中引入一个固定的收敛因子μ_n，这是因为所有的倒数都是基于平方误差的瞬时值而不是均方误差(MSE)。对于NLMS算法，当输入信号具有强相关性时，LMS算法及NLMS算法的收敛速度将急剧下降。因此对进入自适应滤波器的输入信号首先进行解相关预处理，再对自适应滤波器进行归一化LMS，便得解相关归一化LMS(DNLMS)即用式(4)代替式(3)：



2 基于FPGA的系统开发流程

在早期PFGA的DSP系统设计过程中，DSP开发者直接使用VHDL或Verilog HDL语音进行开发。这种开发难度较大，开发效率较低，为了克服这些问题，出现了许多新的基于FPGA的DSP开发工具，如Altera公司的DSP Builder、Xilinx公司的System Generator等。图1是Altera公司的FPGA系统级开发流程。



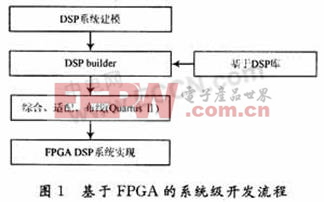
DSP Builder是Altera公司推出的一个面向DSP开发的系统级工具。它是作为Matlab／Simuli-nk的一个工具箱出现的。它从利用Matlab建立DSP电路模型开始。电路模型可方便地利用Simulink与DSPBuilder中提供的功能模块和IP核进行设计。电路中的功能模块和IP的技术参数、数据格式、数据类型和总线宽度等都能直接设置。电路模型建立后就能进行系统级的仿真。仿真通过后可以运行Signal Compiler，将模型转化成RTL级的VHDL代码和Tcl(工具命令语言)脚本语言。调用QuartusⅡ进行编译，QuartusⅡ根据网表文件及设置的优化约束条件进行布线布局和优化设计的适配，最后生成编程文件和仿真文件。

3 系统建模与仿真

根据DNLMS算法的思想，结合FPGA硬件设计的特点。


NLMS算法主要包括延时模块，乘法模块，加法模块，除法模块等。为了让整个系统看起来清晰，降低原理图的复杂性，也便于多次应用，本文将几个多次使用的模块封装成子模块。下面将对各个子模块作简单的介绍。

根据算法的要求，每次新的数据x(n)输入，数据T，S，M都需要重新更新一次，计算量大，消耗的乘法块多。为了解决这个问题。根据T，S，M的运算特点，每次更新只需要一个乘法块和一次加法，就能完成8次乘法和一次加法的运算。具体子模块如图2所示。



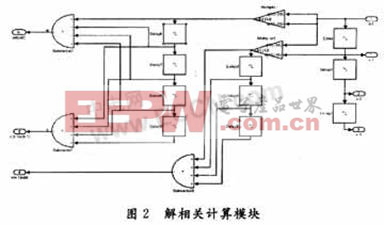
通过图2的优化，对于8阶滤波器，乘法块的使用从24个减少到2个，计算速度将得到很大的提高。ω的迭代运算通过图3实现。



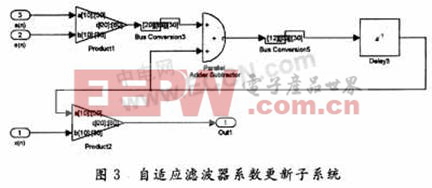
在顶层模块的设计中，加入了PLL模块和SignalComplier，根据各模块仿真周期，在PLL模块中设置好不同的周期，利用Simulink中的颜色标识采样频率的高低。顶层文件的设计如图4所示。

在顶层结构图中，子模块8为方程(9)的实现过程。



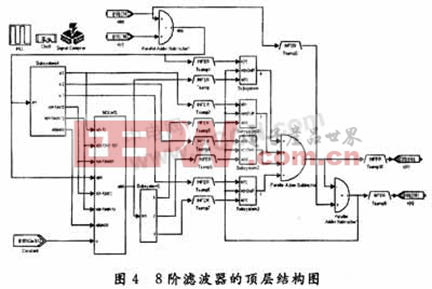
4 计算机仿真

为了充分模拟相关性较强的信号，在输入端加如下的信号源：

x(n)=0.99x(n-1)+v(n)

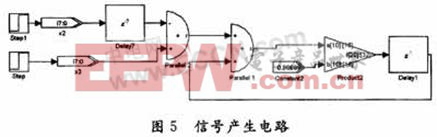
式中：v(n)为高斯白噪声；x(n)的初始值为500，具体的产生电路如图5所示。



信号产生波形以及加噪后的仿真波形如图6所示。


通过滤波器滤波的结果如图7所示。



在图7的信号依次为参考信号、加噪声信号、误差信号和滤波信号。滤波效果良好，对于强相关的信号，也有很好的滤波效果。通过QuartusⅡ编译，滤器器的速度为35.24 MHz，编译后生产如图8所示的块，它作为一个符号模块可供更高级系统设计时调用，通过对该块的修改和增加滤波器的阶数，可以实现对语音的回声消除。

5结 语

自适应滤波器的研究是近年来研究的热门方向，在PFGA中实现高速的自适应滤波器的设计更是一个热点，在此采用DSP Builder系统建模的方法，在FPGA中实现了归一化LMS算法，实验结果表明：用DSPBuilder设计的8阶DNLMS算法比用底层的VHDL代码设计效率更高，灵活性更大，速度更快。同样比通用的DSP芯片设计的8阶NLMS滤波器处理速度快了20多倍。如果将8阶NLMS滤波器扩展到512阶或者1 024阶，可以很好地应用于自适应回声消除等很多自适应滤波的领域。故有一定的参考价值。