Turbo码特点及应用分析

可有效地抑制短波信道中多径时延、频率选择性衰落、人为干扰与噪声带来的不利影响。国内在Turbo码的研究领域也取得了一定的成果和进展，西安电子科技大学综合业务网国家重点试验室在Turbo码的理论和应用研究方面取得了很多研究成果。此外，清华大学、北京邮电大学和上海交通大学等高校都在进行Turbo码相关的其它关键技术的研究方面取得一定的进展。深圳华为公司等在推动Turbo码在移动通信系统中的应用方面起了积极的作用。

编码原理

Turbo 码最先是由C. Beηou等提出的。它实际上是一种并行级联卷积码(Parallel Concatenated Convolutional Codes)。Turbo 码编码器是由两个反馈的系统卷积编码器通过一个交织器并行连接而成，编码后的校验位经过删余阵，从而产生不同的码率的码字。如图所示：信息序列u={u1,u2,……,uN}经过交织器形成一个新序列u'={u1',u2',……,uN'}(长度与内容没变，但比特位经过重新排列)，u 和u'分别传送到两个分量编码器(RSC1与RSC2) ，一般情况下，这两个分量编码器结构相同，生成序列X和X,为了提高码率，序列X和X需要经过删余器，采用删余(puncturing)技术从这两个校验序列中周期的删除一些校验位，形成校验序列X,X,与未编码序列X'经过复用调制后，生成了Turbo码序列X.

1. 分量码的选择

Turbo 码的一个重要特点是它的分量码采用递归系统卷积码(RSC，Recursive Systematic Convolutional code) ，这也是它性能优越的一个重要原因。之所以选择RSC编码器作为Turbo码的子码主要有以下原因：

首先，RSC码具有系统码的优点。这一特性使用户在译码时无需变换码字而直接对接收的码字进行译码，所以，递归系统卷积码( RSC)对于非系统卷积码( NSC )而言译码简单、快速。

其次，从差错控制编码的相关文献中可知，非系统卷积码( NSC )的BER性能在高信噪比时比约束长度相同的非递归系统码要好，而在低信噪比时情况却正好相反。递归系统卷积码综合了NSC码和非递归系统卷积码的特性，且然它与NSC码具有相同的trellis结构和自由距离，但是在高码率(R≥2/3)的情况下，对任何信噪比，它的性能均比等效的NSC码要好。由于系统递归卷积码具有以上特点，并且能改善无码率，所以通常选择RSC码作为Turbo码的子编码器。

递归系统卷权码(RSC)不同于一般的卷积码器在于其结构中不仅有向前结构，还有向后反馈结构，在下图中可以看出。

Turbo码　　RSC 编码器一般有2-5 级移位寄存器， 用生成多项式表示为：

式中，1表示系统比特，gl 和g2分别表示编码器的前馈多项式和反馈多项式。

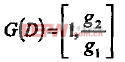
Turbo码　　用RSC码构成Turbo码的分量码的码率R为：

式中：R1，R2为构成Turbo 码的分量码的码率，在经删余后，分量RSC1和RSC2的码率可以不同。

Turbo 码的最大似然译码性能分析出，Turbo 码在高信噪比下的性能主要由它的自由距离所决定。因为Turbo码的自由距离主要由重量为2的输入信息序列所产生的码字间的最小距离所决定，用本原多项式作为反馈连接多项式的分量编码器所产生的码字的最小重量为最大，因此当Turbo码交织器的大小给定后，如果分量码的反馈连接多项式采用本原多项式，则Turbo码的自由距离会增加，从而Turbo码在高斯信噪比情况下的“错误平层(errorfloor)”会降低。错误平层效应指的是在中高信噪比情况下，误码曲线变平。也就是说，即使是再增大信噪比，无码率也降不下来(一般的系统，比如说是BPSK的误码曲线，误码率随着信噪比的增大是单调下降的) 。

2. 交织器的设计

交织器是影响Turbo码性能的一个关键因素，它可以便Turbo码的距离谱细化，即码重分布更为集中。它的特性的好坏直接关系着Turbo码的性能。

编码器中交织器的使用是实现Turbo码近似随机编码的关键。交织器实际上是一个一一映射函数，作用是将输入信息序列中的比特位置进行重置，以减小分量编码器输出校验序列的相关性和提高码重。通常在输入信息序列较长时可以采用近似随机的映射方式，相应的交织器称为伪随机交织器。由于在具体的通信系统中采用Turbo码时交织器必须具有固定的结构，同时是基于信息序列的，因此在一定条件下可以把Turbo码看成一类特殊的分组码来简化分析。交织是对信息序列加以重新排列的一个过程。如果定义一个集合A ， A={1，2，…，N} 。则交织器可以定义为一个一一对应的映射函数π(A-->A):J=π(i)，(i,j属于A) 这里的i ，j 分别是未交织序列C 和交织序列C' 中的元素标号。映射函数可以表示为πN = (π(1),π(2),π(3),…,π(N)) 。其原理如图

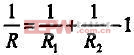
Turbo