不采用自适应算法的智能天线系统分析

当加权信号已知时，阵列天线方向图可由式(1)算出.式中g(θ)为阵列方向图；ωm为第m路信号的加权值；φm(θ)是信号从空间角度到达阵列单元m时的相位差.
　　图2是一个阵元间距为半波长的8元圆形自适应阵列在1用户、10干扰用户的一种随机分布通信环境下对应的方向图.由图2可见，系统在干扰方向形成凹点，并在所需信号方向形成峰值.通常自适应算法在无干扰信号的其它角度上也可能出现峰值.

图2　自适应方向图

　　图3是等旁瓣针状波束方向图，等旁瓣针状波束方向图也可由(1)式计算出.等旁瓣方向图与自适应方向图的不同在于加权信号产生的方式不同，等旁瓣方向图的加权值是预先计算好的.等旁瓣智能天线系统工作时，首先需要通过测向算法测定信号的到达角度(DOA)，然后通过选取合适的加权，将方向图的主瓣指向用户到达方向.这类智能天线对于处于非主瓣区域的干扰，是通过低的等旁瓣电平来确保抑制的.对于处于主瓣区域内的干扰，采用等旁瓣针状智能天线系统将无法抑制.由于系统方向图主瓣宽度是由天线阵列口径决定的，所以自适应智能天线对于主瓣内的干扰信号抑制能力也是很有限的.与自适应智能天线相比，等旁瓣智能天线无需迭代，响应速度快，而且这种方案的鲁棒性更好.

三、智能天线系统对照仿真结果
　　本节分别给出了采用自适应方向图(Applebaum算法［11］)、-10dB等旁瓣针状波束方向图(如图4虚线)、-15dB等旁瓣针状波束方向图(如图3)、-20dB等旁瓣针状波束方向图(如图4实线)的四种智能天线系统性能的仿真结果.仿真所用系统采用相邻阵元间距为半波长的8元圆形阵列，假设阵列采用各向同性单元.仿真时对于自适应智能天线不考虑迭代过程，为系统最终稳态结果.

图4　-10dB、-20dB等旁瓣针状波束方向图

本文仿真均假设CDMA系统具有理想的功率控制，系统的扩频系数为128，无话音激励.小区内除用户外无其它干扰，无邻近小区干扰，无多径干扰.系统的门限值Eb/N=6dB.根据上述假设一个采用全向天线的基站可支持的最大用户数为32.
　　图5给出了一个门限值为6dB的32用户CDMA系统中，在基站引入四种不同智能天线后，系统Eb/N的累积概率分布.图5中每条曲线都是10000次随机用户分布的统计结果.由图5可以看出，采用智能天线以后，系统的Eb/N得到了显著的提高.这表明，在不增加用户数目的条件下，采用智能天线可以减少系统所需信号功率、增加基站覆盖面积。当出界概率为0.01时，采用自适应方向图、-10dB等旁瓣针状波束方向图、-15dB等旁瓣针状波束方向图、-20dB等旁瓣针状波束方向图的四种智能天线系统，分别比采用全向天线的系统提高5.25dB、4.75dB、5.05dB、4.45dB.

图5　32用户时四种智能天线系统的累积概率分布

　　图6分别给出了利用四种智能天线扩容的系统，在不同用户数时系统Eb/N低于门限值(6dB)的出界概率分布.图6曲线中每一个点都是10000次随机用户分布的统计结果.在0.01的出界概率下，采用自适应方向图、-10dB等旁瓣针状波束方向图、-15dB等旁瓣针状波束方向图、-20dB等旁瓣针状波束方向图的四种智能天线系统的扩容能力分别为采用全向天线系统的6.81、4.81、6.62、5.66倍.

图7给出了一个8单元等旁瓣针状波束方向图智能天线，当Eb/N＜6的出界概率取0.01时，采用不同旁瓣电平方向图的智能天线系统所能支持的用户数曲线.图中虚线为自适应智能天线所能支持的用户数：218.由图7可见，当旁瓣电平为-20dB时，系统可以支持的用户数为181.随着针状波束方向图旁瓣电平的升高，系统容量增加，当旁瓣电平为-15dB时，系统可以支持的用户数达到最大值：213，仅比采用自适应智能天线的系统少5个.当旁瓣电平超过-15dB以后，系统容量将随着针状波束方向图旁瓣电平的升高而减小，当旁瓣电平为-10dB时，系统可以支持的用户数为153.

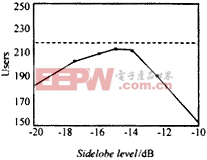
　　图7　智能天线扩容用户数比方向图旁瓣电平

从图6、图7还可以发现，采用-15dB等旁瓣方向图的智能天线系统和采用自适应智能天线有着近似的扩容能力.为了解释这一现象，在图8中给出了当所需信号来向为180度，其它200个干扰用户随机分布时，自适应算法得出的方向图.由图8可知，在干扰数目远大于阵列单元数时，自适应算法得到的方向图(图8)和-15等旁瓣方向图(图3)具有相似的主瓣宽度及旁瓣电平.这一现象可以用自适应算法的原理来解释，当干扰数目少于阵列单元数时，自适应算法可以产生凹点将干扰完全抑制掉.当干扰数目远大于阵列单元数时，因为干扰已遍布于圆周各方向，此时自适应算法已无法通过形成凹点来进行干扰抑制，它只能