基于双闭环模糊PID控制器的开关电源控制

电压调节模块（Voltage Regulator Module，VRM）具有低压大电流输出、快速负载变化响应、高输出稳定度等特点，主要应用于CPU等对供电电源有特殊要求的集成电路芯片的供电。然而随着集成电路技术的迅速发展，晶体管体积迅速减小、单芯片晶体管数迅速增加。这样的半导体制造技术发展趋势已经使得集成电路芯片的供电电压越来越低，负载电流越来越大，负载变化速度越来越快、幅度越来越大。集成电路芯片这样的越来越严酷的供电要求需要VRM 的性能有新的提升。同时性能的提升需要传统控制方法有新的发展和变化。

传统的模拟控制器自Unitrode公司推出UC1842系列以来便通常采用双闭环控制方法。在这种控制器中需要一定的三角波信号作为峰值电流控制模式，或V2控制模式的控制内环输入信号。故在这样的控制律下一般采用输出滤波电感的电流纹波或输出滤波电容的电压纹波作为控制器内环反馈信号。但采用输出滤波电感的电流纹波信号作为控制器输入使控制器无法直接获得负载电流信号。所以该方法在采样环节存在固有的响应延迟问题。而采用输出滤波电容的电压纹波信号作为控制器反馈输入信号虽然可加快负载变化的反馈速度。但随着集成电路供电电压的不断降低，其对电源输出电压的纹波要求不断提高，输出电压纹波必须越来越小。从而输出滤波电容的电压纹波作为控制器的反馈信号必然越来越微弱，信噪比越来越低，越来越容易受到外部干扰。所以传统的双闭环控制律存在一定的缺陷，同时这一缺陷已经越来越无法适应集成电路工业对供电需求的发展。开关电源是一种非常典型的非线性系统，无法建立精确的模型。于此同时模糊PID双闭环控制器，图1作为一种优秀的线性与非线性控制相结合的控制方法具有鲁棒性强，不需要对控制对象准确建模等优点得到了广泛的应用。


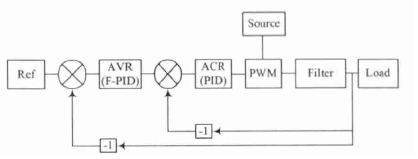
图1 控制系统框图

本文基于Buck变换器提出了一种采用输出电压、输出电流进行双闭环控制的模糊PID（F-PID）控制方法。并通过Matlab/Simulink和Cadence PSpice联合仿真验证了该新型控制方法具有很好的稳定和瞬态响应性能。  
        
1 双闭环F-PID 控制器的设计与实现

本文提出的控制方法直接以负载电流作为反馈量直接控制控制器的占空比输出值，从而避免了传统控制器由于电流采样点位置而造成的问题。

Matlab作为领先的控制算法设计仿真工具，特别是其中包含有模糊控制工具箱（Fuzzy Logic Toolbox）和Simulink设计仿真工具。所以本文中采用Matlab作为控制系统的控制器部分的设计仿真工具。

本控制器的SimuLink框图如图2。其中输出电压标定后作为外环的反馈量以稳定输出电压，输出电流标定后作为内环的反馈量以加快负载变化响应。外环电压控制器即AVR采用F-PID控制器而内环电流控制器ACR采用传统的PID控制器以达到控制器复杂度和性能的折中。ACR的输出经过PWM调制后作为Buck变换器MOSFET的驱动信号。


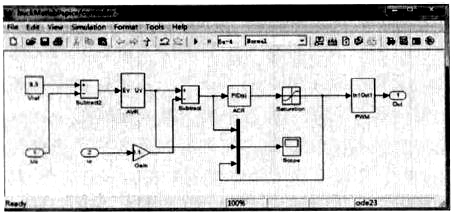
图2 控制器模块

本控制器为了满足VRM对于输出电压精确度的高要求，遂让F-PID控制器工作电压区间较小以提高输出电压精确度。AVR采用F-PID和传统PID的双控制器相互切换的结构，如图3所示。其中传统PID控制器在输出电压误差非常大时进行控制，F-PID控制器在输出电压误差在一定限度内时进行控制。F-PID控制器中的模糊控制器采用典型的两输入三输出设计，如图4所示。输入量分别为电压误差E 和电压误差变化率EC。输出量分别为传统PID控制器的KP，KI，KD的调整系数KKP，KKI，KKD。这样可以使模糊控制器自适应PID参数的设定值，而不用一同调节其中参数。由于直接由变换器输出电压进行微分得到的直接误差变化率极易受外部干扰出现很大的尖峰且直接误差变化率变化范围非常大达到正负1e13以上。所以本课题没有采用微分得到的直接误差变化率作为模糊控制器EC输入信号，而是对其采取了取常用对数并保持原来正负的方法重新标定，如图5所示。在微分前加入低通滤波器以及在微分后加入一阶采样保持器的方法滤除过大尖峰的办法弱化并消除干扰的影响。


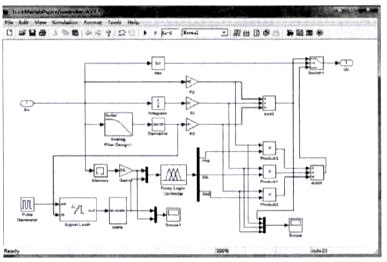
图3 AVR模块


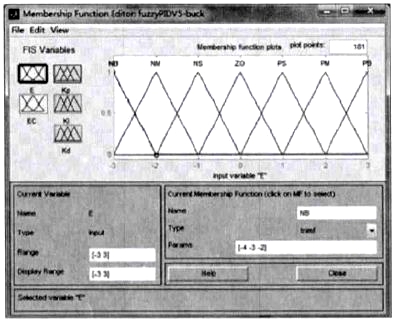
图4 隶属度函数


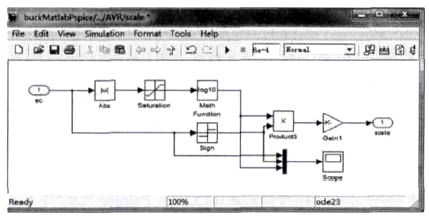
图5 EC标度模块

模糊控制器采用Mamdani型。输入输出变量的隶属度函数均为线性，模糊子集为{NB，NM，NS，ZE，PS，PM，PB}，子集中的元素分别代表负大，负中，负小，零，正小，正中，正大。输入量的论域为[-3，3]，输出量的论域为[0，6]。模糊控制的规则表如图6所示。

ACR采用常规PID控制器以快速响应输出电流的变化，如图7所示。PWM调制时通过调整锯齿波的大小变化范围设置稳态时的输出占空比以加快稳定。


图6 KP，KI，KD规则表


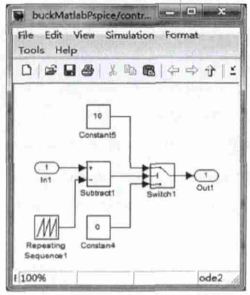
图7 PWM模块
        
2 Buck 变换器与控制器的联合仿真

Cadence/Pspice 是最常用的功率电路仿真环境之一，且其提供了极为便利的和Matlab进行联合仿真的接口，即Matlab/Simulink 中的SLPS模块。所以本控制系统中Buck变换的设计和仿真在Pspice环境下进行。仿真以14~22 V 直流输入3.3 V/（0~10 A）直流输出为Buck变换器输入输出指标，其中Lo=30 μH，Co=220 μF，如图8，图9所示。


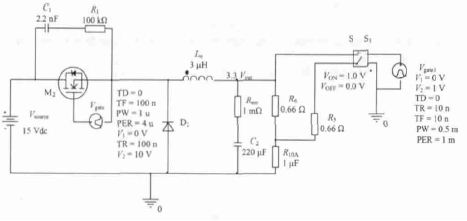
图8 Buck变换器


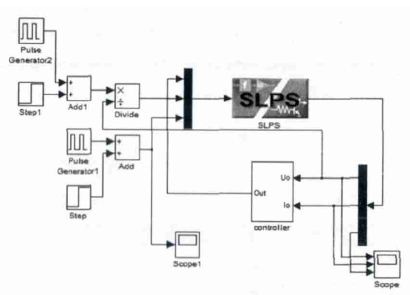
图9 仿真界面

3 仿真结果

本试验分别在电阻、电流负载满载启动并半载到满载阶跃变化以及在各种负载类型下输入电压从额定最低值阶跃跳变到最大值的情况下进行了测试以检验控制器的性能，如图10所示。

由双闭环模糊PID控制器控制的Buck变换器在正常运行中任何的负载端或输入端的变化对输出电压的影响均极为有限。其中当输入端由额定最低输入电压跃变至额定最高输入电压，即变化57%时，Buck变换器3.3 V输出电压有1%左右的变化；当负载电流进行半载和满载之间的阶跃变化时3.3 V 输出电压有