用于风力发电系统中的仿真技术
时间:10-06
来源:互联网
点击:
2.1 典型风力发电机组的仿真模型总体结构
在风电场中得到广泛应用的恒速风力机如图1 所示[2],异步发电机将风轮吸收的机械能转化成电能,发电机转速随发电量的变化而在一定范围内变化,因转速变化范围很小(1% 左右),通常称为恒速系统。恒速系统通常选用失速型调节方式。
上述两种风力发电机组的仿真模型的总体结构分别表示在图3 和图4 中[3] ,变速风力机的控制系统要比恒速系统复杂得多,其仿真模型相应增加了桨距角、转速、端电压等控制器子模型和变频器的仿真模型。
描述风能特性的参数主要有风速、风向和风密度。风的密度主要取决于风机所处的地理位置,气候变化也会产生一定影响,对于特定风机而言,风密度可以直接取自测量数据,并可以忽略密度的变化;针对研究型的仿真应用,风向的变动可不予考虑,即假定风力机一直跟踪风向的变化。因此,我们主要关注风速的变化特性。
风因大气环流形成,风速是一个典型的随机变量。若不考虑风的方向性,风速是其空间坐标位置和时间的函数,即v=f(x,y,z,t) 。我们将描述某一区域风速的空域、时域分布变化特性的模型又称为风场模型(Wind Field Model)。严格说来,各空间位置上的风速因风的随机性、风场地形等因素影响而各不相同,因此,要建立一个准确的风场模型几乎是不可能的,需要进行一定的简化处理。
若风场的地形相对平坦,周边空旷,则基本可以认为在同一高度层上整个风场内各点的风速是相同的,这样可以将风场风速的三维空间模型简化为沿高度方向变化的一维模型。对于空间分布广,且地形复杂的大型风电场,可以将整个风场划分成几个区域,针对不同区域的风能特点建立简化的一维空间模型,形成分段集总式一维模型。风速空域模型转化为研究风速沿地平面高度方向的变化规律,借助空气动力学理论和风场测量数据,模型不难建立。
在时间维度上,大时期尺度(小时、天)的风速变化范围很大,且没有规律可循,只能根据风场监测记录数据拟合出风速变化模型。对于绝大多数仿真应用而言,我们不太关心大时间尺度的风速变化,而重点关注小时间尺度上的风速变化特性。在小时间尺度上观察,风速随时间的变化呈现出脉动变化的特点,即风速均值在一段时间内基本不变,风速在均值附近波动,国内外学者据此提出了各种描述风频分布的方法,如概率分布模型、瑞利分布模型、对数正态分布模型等[1] 。
需要说明的是,在建立风电场内各风力发电机组的仿真模型时,需要考虑到风力机的尾流效应,即上游风力机对下游风力机流入风速的影响,影响关系和程度取决于风向、风速和风机安装位置关系,此时,风力机的输出机械能通常由尾流系数予以校正。
2.3 风力机模型[4]
风力机实际能够获得的机械功输出为:
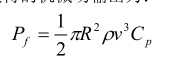
(1)
式中, R 、ρ、 v 和Cp分别为风轮半径、空气密度、风速和风能利用系数。
Cp代表风力机能够从风能中提取出机械能的程度,它取决于风力机叶片的结构和运行状态,其数值由风机厂家提供。Cp主要是叶尖速比λ和桨距角β的函数,即 :Cp=f(λ,β),对于投入运行的风力机,叶片的洁净程度对Cp的影响很大,譬如叶片结冰、污物聚集等会改变叶片的气动外型,进而降低风能利用系数的数值。
在风电场中得到广泛应用的恒速风力机如图1 所示[2],异步发电机将风轮吸收的机械能转化成电能,发电机转速随发电量的变化而在一定范围内变化,因转速变化范围很小(1% 左右),通常称为恒速系统。恒速系统通常选用失速型调节方式。
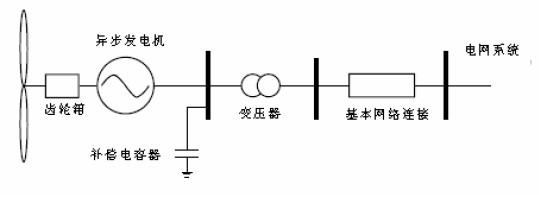
图 1 恒速风力机系统示意图
一种典型的变速风力发电机组见图2,它采用双馈异步发电机(DFIG)。发电机的定子线圈直接与电网相连,转子线圈则通过滑环和电力电子逆变器与电网连接。因此,当风速变化引起发电机转速变化时,通过控制转子电流的频率,可保持定子频率的恒定,进而实现风力发电机组的变速运行。在高风速条件下,通过调整叶片桨距限制风力机的输出功率。上述两种风力发电机组的仿真模型的总体结构分别表示在图3 和图4 中[3] ,变速风力机的控制系统要比恒速系统复杂得多,其仿真模型相应增加了桨距角、转速、端电压等控制器子模型和变频器的仿真模型。
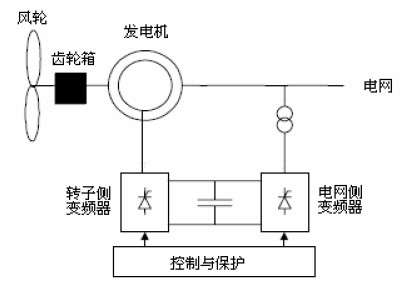
图 2 典型的双馈发电机组系统示意图
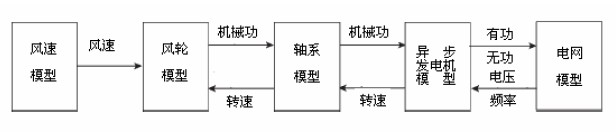
图 3 恒速风力机仿真模型的总体结构

图 4 变速风力机仿真模型的总体结构
2.2 风能特性模型描述风能特性的参数主要有风速、风向和风密度。风的密度主要取决于风机所处的地理位置,气候变化也会产生一定影响,对于特定风机而言,风密度可以直接取自测量数据,并可以忽略密度的变化;针对研究型的仿真应用,风向的变动可不予考虑,即假定风力机一直跟踪风向的变化。因此,我们主要关注风速的变化特性。
风因大气环流形成,风速是一个典型的随机变量。若不考虑风的方向性,风速是其空间坐标位置和时间的函数,即v=f(x,y,z,t) 。我们将描述某一区域风速的空域、时域分布变化特性的模型又称为风场模型(Wind Field Model)。严格说来,各空间位置上的风速因风的随机性、风场地形等因素影响而各不相同,因此,要建立一个准确的风场模型几乎是不可能的,需要进行一定的简化处理。
若风场的地形相对平坦,周边空旷,则基本可以认为在同一高度层上整个风场内各点的风速是相同的,这样可以将风场风速的三维空间模型简化为沿高度方向变化的一维模型。对于空间分布广,且地形复杂的大型风电场,可以将整个风场划分成几个区域,针对不同区域的风能特点建立简化的一维空间模型,形成分段集总式一维模型。风速空域模型转化为研究风速沿地平面高度方向的变化规律,借助空气动力学理论和风场测量数据,模型不难建立。
在时间维度上,大时期尺度(小时、天)的风速变化范围很大,且没有规律可循,只能根据风场监测记录数据拟合出风速变化模型。对于绝大多数仿真应用而言,我们不太关心大时间尺度的风速变化,而重点关注小时间尺度上的风速变化特性。在小时间尺度上观察,风速随时间的变化呈现出脉动变化的特点,即风速均值在一段时间内基本不变,风速在均值附近波动,国内外学者据此提出了各种描述风频分布的方法,如概率分布模型、瑞利分布模型、对数正态分布模型等[1] 。
需要说明的是,在建立风电场内各风力发电机组的仿真模型时,需要考虑到风力机的尾流效应,即上游风力机对下游风力机流入风速的影响,影响关系和程度取决于风向、风速和风机安装位置关系,此时,风力机的输出机械能通常由尾流系数予以校正。
2.3 风力机模型[4]
风力机实际能够获得的机械功输出为:
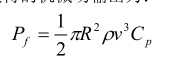
(1)
式中, R 、ρ、 v 和Cp分别为风轮半径、空气密度、风速和风能利用系数。
Cp代表风力机能够从风能中提取出机械能的程度,它取决于风力机叶片的结构和运行状态,其数值由风机厂家提供。Cp主要是叶尖速比λ和桨距角β的函数,即 :Cp=f(λ,β),对于投入运行的风力机,叶片的洁净程度对Cp的影响很大,譬如叶片结冰、污物聚集等会改变叶片的气动外型,进而降低风能利用系数的数值。
- 负载点降压稳压器及其稳定性检查方法(07-19)
- 电源SOC:或许好用的“疯狂”创意(07-24)
- DC-DC变换器中一种高性能振荡电路的设计(04-08)
- 驱动HB LED的分立元件降压变换器(08-04)
- DC/DC电源管理应用中的功率MOSFET的热分析方法(12-10)
- 基于BCM的有源功率因数校正电路的实现(03-12)
