电机软启动自整定模糊控制器的研究与设计
时间:08-10
来源:互联网
点击:
1 引言
三相异步电机应用广泛,但是直接全压启动时电流很大(6-8倍),传统的方法采用如Y-△转换、自耦变压器及定子回路串电抗等降压启动方法来减小启动电流,启动设备的启动参数一般无法调整,使其负载的适应性较差。而电机软启动的方式具备无冲击电流、启动参数可调、有软停机功能、轻载节能等优点逐渐被广泛应用。各启动方式对电网的影响示意图如图1所示。
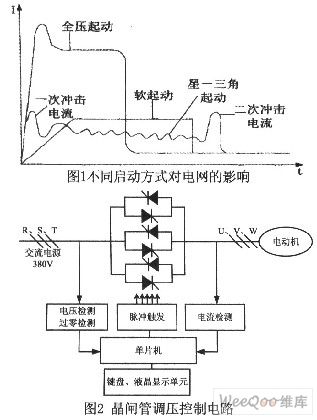
目前,软启动方式主要采用晶闸管交流调压的方法。在电动机起动过程中通过控制晶闸管触发角的大小,可使电动机的定子端电压和起动电流根据工作要求设定的规律进行变化。电动机的起动方式和起动电流均可任意调整和设置,使之处于最佳的起动过程。常用的晶闸管调压控制电路如图2所示。

本文介绍参数自整定模糊控制技术在限流软启动中的应用,利用模糊推理、模糊决策对电动机启动过程中电流大小进行控制,实现了系统平稳启动。
2 模糊控制的方案
电机软启动传统的方法是采用闭环PID控制对电动机进行限流软起动。但是由于异步电动机启动过程是非线性时变系统,采用PID闭环控制并不能很好的解决异步电动机起动过程中电流冲击问题。所以,本文采用快速调节能力强的参数自整定模糊控制技术应用于电机软启动的控制中。模糊控制作为智能控制的一种方法,它最大的优点就是不依赖于被控对象的精确的数学模型,能够克服系统非线性因素的影响,对被控对象参数的变化具有较强的鲁棒性。
3 基于自整定模糊控制系统的结构
常规模糊控制器具有响应时间短,超调量小,鲁棒性好,适于非线性时变的复杂系统,建立模型相对容易等优点。
模糊控制器具有良好的动态品质,同时也还存在一些问题:首先,常规的模糊控制器的控制规则建立之后就固定不变,难以获得最优控制指标。相对于电动机软起动过程这类复杂的被控对象,采用这种控制器不能获得预期的控制效果,而且适应系统和环境变化的能力差。
为此我们采用参数自整定模糊控制技术,在运行过程中根据实际偏差和偏差变化率的大小,控制器选取不同的Ka、Kb、Kc以满足动、静态性能的不同要求。而且,基于量化、比例因子自调整方法,由于算法简单高效,控制效果较好,很适合电动机软启动这类对控制的实时性要求较高的系统。
如图3所示,考虑系统控制情况,选电流偏差e、偏差变化率ec为输入变量、晶闸管触发角的变化值a为输出量。当量化因子Ke、Kec和比例因子取为常数时,可调整因子K1、K2、K3通过寻优的方法,不断更新K1、K2、K3的值从而完成模糊控制规则的自调整,使模糊控制系统有最佳的动态性能。
4 模糊控制参数的选择
4.1 模糊隶属函数
本模糊控制器采用二维模糊控制,主模糊控制单元和模糊参数寻优控制单元都以异步电动机的输出电流与期望值的偏差e及偏差变化率ec作为输入变量,其中主模糊控制单元输出变量为晶闸管触发角a的变化值。模糊参数寻优控制单元的输出可调整因子K1、K2、K3分别表示量化因子Ke、Kec以及比例因子Ka的调整系数值。
e、ec以及模拟控制器的输出a的论域取{-4,-3,-2,-1,0,+1,+2,+3,+4),将其大小量化为9个等级。在模糊控制区内将电流偏差分为7个模糊子集,即Ke的语言变量{负大,负中,负小,零,正小,正中,正大),简记为{NB,NM,NS,ZO,PS,PM,PB)。
为了运算简便,对于输入输出变量采用简单的三角形隶属度函数。隶属度函数赋值表如下表所示:

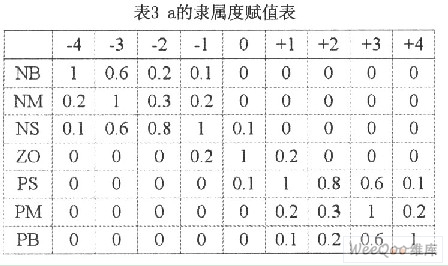
4.2 模糊控制规则
综合考虑电流偏差Ke和电流偏差的变化率Kec2羞两个信号,采用的模糊推理规则的形式如下:


相应的模糊控制规则总表如表4所示
解模糊使用的重心法,又称加权平均法。其解模糊公式如下:
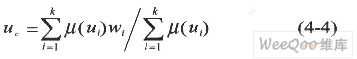
4.3 模糊控制器参数自整定
在启动过程中遵循的自整定规则如下:
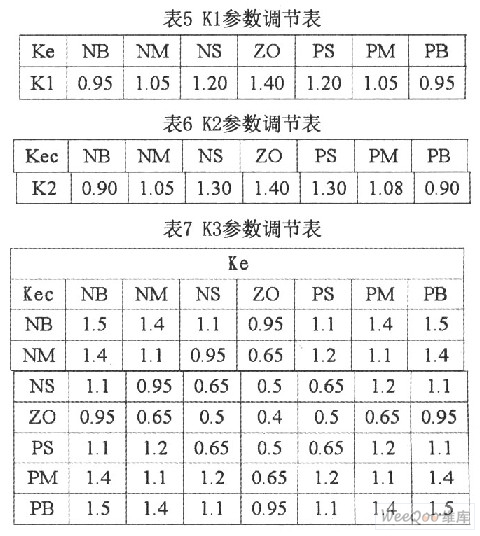
当e和ec较大时,缩小K1和K2,降低对大偏差的分辨率,减少偏差,缩短过渡过程时间。当e和ec较小时,系统已接近稳态,这时应增大K1和K2,提高系统对小偏差的分辨率,提高控制的灵敏度;当误差e较大,且与误差变化ec符号相反时,应适当增大控制器k3的大小。当误差e较大,且与误差变化ec符号相同时,系统响应正加速偏离设定值,为减小这种不利趋势,也应适当减小K3。系统响应在设定值附近时(此时误差e较小),为防止产生较大的超调或欠调,K3应该具有较宽的变化范围。适当减小比例因子以减小超调。经过多次仿真和实验,随着偏差Ke和偏差变化率Kec的变化,K1、K2和K3分别按表5、6、7取值,可以得到理想的控制结果。
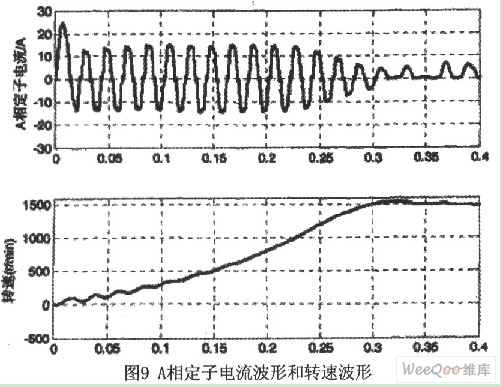
5 系统仿真与分析
利用MATLAB的Simulink和Simpowersystems、FuzzyLogicToolbox等工具进行的系统仿真。
5.1 仿真模型的建立
结合上述的方法建立的自整定模糊控制器仿真模型如图4:

结合三相电源模块、同步环节模块、脉冲发生环节模块、三相交流调压环节模块以及控制环节得到整体软启动仿真模型如图5。

将采用传统PID控制器获得的响应曲线和采用自整定模糊控制器获得的响应曲线对比可知,采用自整定模糊控制器获得的控制效果更为理想,具体表现为:超调量较小、启动过程平稳,其输出量几乎和给定量达到重合。通过以上的对比可知,自整定模糊控制器的控制性能优于传统PID控制的控制性能,同时,也说明了本文设计的自整定模糊控制器获得了较好的控制效果。
6 小结
本章结合电动机软启动的特性在吸取自适应和模糊控制算法各自优点的基础上,介绍了限流软启动自整定模糊控制器设计的整个过程;并对整个软启动控制系统进行了动力学建模,最后,利用MATLAB的power system模块库以及Simulink模块库建立仿真模型功能进行了系统仿真,仿真结果表明,自整定模糊能够在软启动控制上取得较好的动、静态性能。
三相异步电机应用广泛,但是直接全压启动时电流很大(6-8倍),传统的方法采用如Y-△转换、自耦变压器及定子回路串电抗等降压启动方法来减小启动电流,启动设备的启动参数一般无法调整,使其负载的适应性较差。而电机软启动的方式具备无冲击电流、启动参数可调、有软停机功能、轻载节能等优点逐渐被广泛应用。各启动方式对电网的影响示意图如图1所示。

目前,软启动方式主要采用晶闸管交流调压的方法。在电动机起动过程中通过控制晶闸管触发角的大小,可使电动机的定子端电压和起动电流根据工作要求设定的规律进行变化。电动机的起动方式和起动电流均可任意调整和设置,使之处于最佳的起动过程。常用的晶闸管调压控制电路如图2所示。

本文介绍参数自整定模糊控制技术在限流软启动中的应用,利用模糊推理、模糊决策对电动机启动过程中电流大小进行控制,实现了系统平稳启动。
2 模糊控制的方案
电机软启动传统的方法是采用闭环PID控制对电动机进行限流软起动。但是由于异步电动机启动过程是非线性时变系统,采用PID闭环控制并不能很好的解决异步电动机起动过程中电流冲击问题。所以,本文采用快速调节能力强的参数自整定模糊控制技术应用于电机软启动的控制中。模糊控制作为智能控制的一种方法,它最大的优点就是不依赖于被控对象的精确的数学模型,能够克服系统非线性因素的影响,对被控对象参数的变化具有较强的鲁棒性。
3 基于自整定模糊控制系统的结构
常规模糊控制器具有响应时间短,超调量小,鲁棒性好,适于非线性时变的复杂系统,建立模型相对容易等优点。
模糊控制器具有良好的动态品质,同时也还存在一些问题:首先,常规的模糊控制器的控制规则建立之后就固定不变,难以获得最优控制指标。相对于电动机软起动过程这类复杂的被控对象,采用这种控制器不能获得预期的控制效果,而且适应系统和环境变化的能力差。
为此我们采用参数自整定模糊控制技术,在运行过程中根据实际偏差和偏差变化率的大小,控制器选取不同的Ka、Kb、Kc以满足动、静态性能的不同要求。而且,基于量化、比例因子自调整方法,由于算法简单高效,控制效果较好,很适合电动机软启动这类对控制的实时性要求较高的系统。
如图3所示,考虑系统控制情况,选电流偏差e、偏差变化率ec为输入变量、晶闸管触发角的变化值a为输出量。当量化因子Ke、Kec和比例因子取为常数时,可调整因子K1、K2、K3通过寻优的方法,不断更新K1、K2、K3的值从而完成模糊控制规则的自调整,使模糊控制系统有最佳的动态性能。
4 模糊控制参数的选择
4.1 模糊隶属函数
本模糊控制器采用二维模糊控制,主模糊控制单元和模糊参数寻优控制单元都以异步电动机的输出电流与期望值的偏差e及偏差变化率ec作为输入变量,其中主模糊控制单元输出变量为晶闸管触发角a的变化值。模糊参数寻优控制单元的输出可调整因子K1、K2、K3分别表示量化因子Ke、Kec以及比例因子Ka的调整系数值。
e、ec以及模拟控制器的输出a的论域取{-4,-3,-2,-1,0,+1,+2,+3,+4),将其大小量化为9个等级。在模糊控制区内将电流偏差分为7个模糊子集,即Ke的语言变量{负大,负中,负小,零,正小,正中,正大),简记为{NB,NM,NS,ZO,PS,PM,PB)。
为了运算简便,对于输入输出变量采用简单的三角形隶属度函数。隶属度函数赋值表如下表所示:


4.2 模糊控制规则
综合考虑电流偏差Ke和电流偏差的变化率Kec2羞两个信号,采用的模糊推理规则的形式如下:


相应的模糊控制规则总表如表4所示
解模糊使用的重心法,又称加权平均法。其解模糊公式如下:
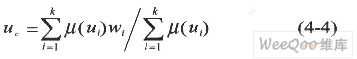
4.3 模糊控制器参数自整定
在启动过程中遵循的自整定规则如下:
当e和ec较大时,缩小K1和K2,降低对大偏差的分辨率,减少偏差,缩短过渡过程时间。当e和ec较小时,系统已接近稳态,这时应增大K1和K2,提高系统对小偏差的分辨率,提高控制的灵敏度;当误差e较大,且与误差变化ec符号相反时,应适当增大控制器k3的大小。当误差e较大,且与误差变化ec符号相同时,系统响应正加速偏离设定值,为减小这种不利趋势,也应适当减小K3。系统响应在设定值附近时(此时误差e较小),为防止产生较大的超调或欠调,K3应该具有较宽的变化范围。适当减小比例因子以减小超调。经过多次仿真和实验,随着偏差Ke和偏差变化率Kec的变化,K1、K2和K3分别按表5、6、7取值,可以得到理想的控制结果。


5 系统仿真与分析
利用MATLAB的Simulink和Simpowersystems、FuzzyLogicToolbox等工具进行的系统仿真。
5.1 仿真模型的建立
结合上述的方法建立的自整定模糊控制器仿真模型如图4:

结合三相电源模块、同步环节模块、脉冲发生环节模块、三相交流调压环节模块以及控制环节得到整体软启动仿真模型如图5。

将采用传统PID控制器获得的响应曲线和采用自整定模糊控制器获得的响应曲线对比可知,采用自整定模糊控制器获得的控制效果更为理想,具体表现为:超调量较小、启动过程平稳,其输出量几乎和给定量达到重合。通过以上的对比可知,自整定模糊控制器的控制性能优于传统PID控制的控制性能,同时,也说明了本文设计的自整定模糊控制器获得了较好的控制效果。
6 小结
本章结合电动机软启动的特性在吸取自适应和模糊控制算法各自优点的基础上,介绍了限流软启动自整定模糊控制器设计的整个过程;并对整个软启动控制系统进行了动力学建模,最后,利用MATLAB的power system模块库以及Simulink模块库建立仿真模型功能进行了系统仿真,仿真结果表明,自整定模糊能够在软启动控制上取得较好的动、静态性能。
电流 变压器 电动机 电压 电路 仿真 电源模块 相关文章:
- 航天器DC/DC变换器的可靠性设计(02-12)
- 基于nRF2401智能小区无线抄表系统集中器设计(04-30)
- 卫星电源分系统可靠性设计与研究(02-12)
- 采用信号调理IC驱动应变片电桥传感器(05-26)
- 解密波音747飞机中的Sperry垂直陀螺仪(05-06)
- 安森美90W太阳能LED街灯高能效解决方案(05-18)
