使用双轴加速度计进行倾斜测量

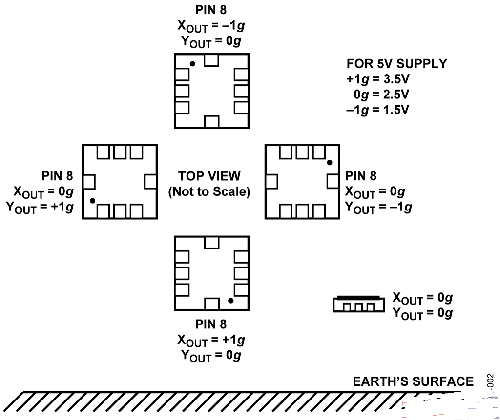
Figure 2. Output Response vs. Orientation

调理ADXL203电压输出

为了处理加速度计数据并计算出角度，必须通过AD7887对信息进行数字化处理。必须确定ADXL203的最差输出电压范围并将其与ADC输入电压范围进行比较。AD7887的输入电压范围为0 V至VDD = 3.3 V.ADXL203的理想输出电压范围为1.5 V至3.5 V.不过，确定此范围时忽略了数种非理想特性。

第一种非理想特性是零g偏置电平。此电压的额定范围为2.4 V至2.6 V，最差情况下会上下偏移100 mV.第二种非理想特性是特定输出的灵敏度，最差规格为960 mV/g至1040 mV/g.通过结合考虑这些误差，就可以计算出ADXL203最差情况的输出范围：

VMAX （+1 g） = （2.6 V） + （1040 mV/g）×（+1 g） = 3.64 V

VMIN （？1 g） = （2.4 V） + （1040 mV/g）×（？1 g） = 1.36 V

既已确定加速度计的输出范围，接下来目标就是操控此范围（VCM = 2.5 V时为1.36 V至3.64 V）来满足ADC输入范围要求。对于双通道工作模式，AD7887输入范围为0 V至VDD（VCM = 1.7 V时为0 V至3.3 V）。四通道AD8608用于构建图1所示的2级调理电路。

第一级提供大小为1.2的信号增益并对共模电压进行电平转换，使其大小变为2 V.第二级提供大小为1.1的信号增益（总信号增益为1.32时）并建立1.7 V共模输出电压。此运算放大器级的输出电压范围就与ADC输入电压范围非常一致，负端和正端分别略有200 mV和100 mV的裕量。

单轴倾斜计算

在此以图3所示的单轴解决方案为例进行说明。根据三角恒等式，X轴上的重力矢量投影会产生输出加速度，大小等于加速度计X轴和水平面之间夹角的正弦值。水平面通常是与重力矢量正交的平面。当重力为理想值1 g时，输出加速度为：

AX， OUT [g] = 1 g×sinθ

利用反正弦函数可以将加速度转换成倾斜角。

θ= sin -1 （AX， OUT [g]/ g）

其中，倾斜角θ单位为弧度。

Figure 3. Single Axis Used for Tilt Sensing

必须注意，使用单轴解决方案时，灵敏度会随水平面和X轴之间的夹角增大而降低。当该角度接近±90°时，灵敏度会趋于0.这点可以从图4中看出，其中绘出了输出加速（以g表示）度与倾斜角之间的关系图。接近±90°时，倾斜角出现很大变化时，输出加速度只会产生很小变化。

必须注意超出范围的信号。加速度计可能会因为振动、冲击或其它突然加速而输出大于±1 g的信号。

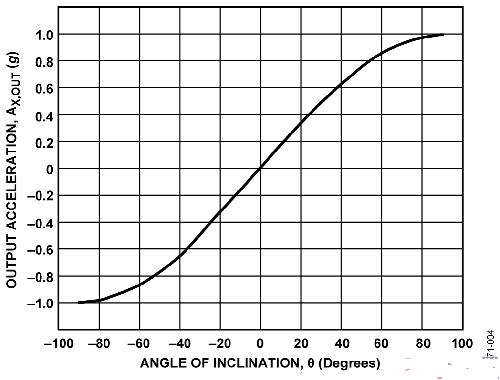
Figure 4. Output Acceleration vs. Angle of Inclination for Single Axis Inclination Sensing

单轴与双轴考虑因素

要解决单轴解决方案中灵敏度随着旋转角度趋于90°而逐渐下降的问题，一种简单的方法是增加一个与原轴正交的轴。增加一个轴对确定倾斜角有三大好处。

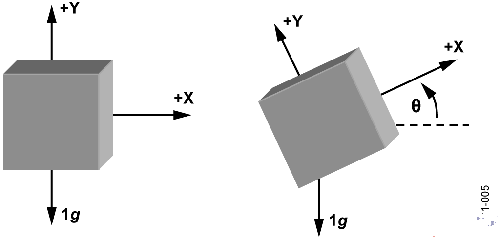
Figure 5. Two Axes Used for Tilt Sensing

增加一个轴的第一大好处在于两个轴相互垂直。在单轴解决方案中，X轴检测到的加速度与倾斜角的正弦值成比例。由于两个轴相互垂直，因此Y轴加速度与倾斜角的余弦值成比例（见图6）。随着一个轴的灵敏度下降，另一个轴的灵敏度会上升。

使用至少两个轴的第二大好处是，与单轴解决方案不同，增加一个轴后，即使第三个轴上存在倾斜，也可以测出精确值。而在单轴解决方案中，只要任何其它轴上存在倾斜，就会造成显著误差。这是因为灵敏度与目标轴上重力的和方根（rss）值成比例。

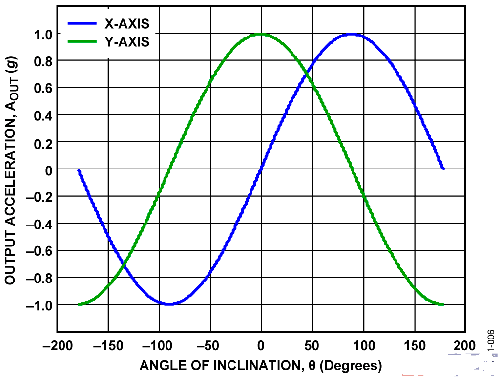
Figure 6. Output Acceleration vs. Angle of Inclination for Dual-Axis Incination Sensing

增加一个轴的第三大好处是，能够区分各个象限并在整个360°弧度范围内测量角度。每个象限都具有与X和Y轴加速度关联的不同符号组合。

如果操作数AX， OUT/AY， OUT为正值，反正切函数会返回第一象限中的值；如果操作数为负值，则反正切函数会返回第四象限中的值。第二象限内的操作数为负值，因此在计算该象限内的角度时应将结果加上180°。第三象限内的操作数为正值，因此在计算该象限内的角度时应从结果中减去180°。而该角度所处的确切象限则可以通过各轴上测得的加速度符号来确定。

双轴倾斜计算

既然系统中增加了一个轴，也就需要重新审视倾斜角的计算方法。简单的方法就是照旧计算X轴，再以类似方式计算Y轴，不过记住要使用角度的余弦。

AX， OUT [g] = 1 g×sinθ

AY， OUT [g] = 1 g×cosθ

利用反正弦函数和反余弦函数将加速度转换成角度。

θ= sin-1 （AX， OUT [g]/ 1 g）

θ= cos-1 （AY， OUT [g]/ 1 g）

其中，倾斜角θ单位为弧度。

但是，更简单的方法是应用三角恒等式并使用这些值的比值，那样可得到如下结果：

其中，倾斜角θ单位为弧度。

校准

在图1所示的加速度计电路设计中，最关键的就是能够校准该系统。如果不进行精确校准而又没有适当的测试程序和设置，该系统的误差将远大于预期值。CN0189 Labview软件包含一个预定义的系统校准程序。接下来，我们将探讨如何校准本系统，以及误差贡献有哪些和为何需要进行校准。

失调误差的影响

首先设想一下，某个双轴解决方案具有完美的灵敏度，但X轴上存在50 mg失调。0°时，X轴读数为50 mg，Y轴读数则为1 g.由此计算得出的角度就是2.9°，因而会造成2.9°的误差。±180°时，X轴的读数为50 mg，Y轴的读数则为？1g.由此计算得出的角度会存在？2.9°的误差。

图7所示为本例中算出的角度和实际角度之间的误差情况。失调引起的误差可能不仅大于系统所需的精度，而且还会发生变化，使简单地通过校准消除误差角变得困难。当多个轴上都存在失调时，这将会变得更为复杂。