便携式功率分析仪设计----键盘设计与校准、调试与测试

便。

第五章校准、调试与测试

任何计量器具由于种种原因都具有不同程度的误差计量器具的误差，只在允许的范围内才能应用，否则将带来错误的计量结果。对于新制的或修理后的计量器具必须用适当等级的计量标准来确定其计量特性是否合格，对于使用中的计量器具必须用适当等级的计量标准对其进行周期检定，另外有些计量器具必须借助适当等级的计量标准来确定其示值和其它计量性能，因此量值传递的必要性是显而易见的。

5.1常用仪器校准方法

微波功率量值传递的关键是减小失配误差。功率的量值传递方法大致可分为四类：

①交替连接比较法：把标准功率计和被校功率计交替接到稳定的信号源上进行校准。这种方法的误差较大，但简单易行，在准确度要求不高的情况下广泛使用。

②单定向耦合器直接比较法：利用定向耦合器-功率检波器组合，提供一个稳幅的低反射系数的等效信号源（图2）。当采用调配措施后，可使等效信号源的反射系数小于0.005，减小失配误差，然后用功率标准对其校准，确定校准系数后可作为传递标准，用来单独校准其他功率计。

③调配反射计法：为了有效地消除失配误差、提高功率测量和量值传递的准确度，1960年开始采用反射计法进行功率量值传递，利用调配反射计技术，有效地将入射波与反射波分开以消除失配误差。但这种方法复杂，技术要求很高。

④功率方程法：1969年G.F.恩金提出一种描述和计算微波系统的"功率方程概念"，用传输的净功率这一基本实数参量替代电路理论中的复数行波波幅来分析和计算微波系统，放宽了对均匀波导，特别是对精密同轴接头的要求，对失配误差的修正提出了一个确定解，克服了电路理论只能估计失配误差极限的缺点。功率方程法采用广义反射计技术的校准系统（图3）。它测量两个实数的失配因子，对失配误差进行精确修正，测量准确度可达到±0.2％。在实际校准测试过程中，我们选用的设计方法较为简单的单定向耦合器直接比较法进行仪器校准，从而生成校准参数。

5.2校准调试功率校准

主要针对A/D采样值与实际功率值间的转换关系和功率的频响误差进行。通过功率测量过程，我们将校准主要分为以下4个部分：通道校准、功率测量校准、频率测量校准、功率频响校准。

5.2.1通道校准

我们在计算功率值时，是利用的A/D采样得到的十六进制表示的电压值，为了获得实际射频信号经过检波模块输出电压值，就必须通过此时A/D采样得到的电压和实际电压的对应关系拟合出实际电压值和A/D前端电压值的曲线。由于在通道设计上我们在A/D之前加入AD8369（可变增益放大器）实现3 dB步长的数字增益调节，所以拟合曲线根据不同衰减挡位进行拟合。

设该功率计的测量范围是-57dBm到+23dBm（频率在10MHz～6GHz）的射频信号。根据检波模块的特性可知，其向后端输出电压范围是0.5V到2.5V，故先固定AD8369的衰减挡位，以4dbm为步进（以得到较为明显的电压变化）从-57dBm到+23dBm分别测出其A/D采样值V A/D与检波器实际输出值V T，然后用最小二乘法进行直线拟合得到一条V A/D和V T之间关系直线。再调整AD8369的信号衰减参数，最后计算得到十六条V A/D和V T之间关系的拟合直线，这样A/D采样值才能较为真实的反应输入采样通道的实际值，这为后面的功率测量值校准提供先决条件。

5.2.2功率测量值校准

在功率计算中，关键部分是测量脉冲调制信号的峰值功率值。此时捕捉到的峰值仅仅是A/D采样得到的十六进制表示的电压值。通过此时电压和功率的对应关系拟合出电压值和功率值的曲线。

由前面的分析可知，经峰值检波后所得包络的峰值与其相应的峰值功率值成线性关系，所以以1dBm为步进从-57dBm到+23dBm分别测出其A/D采样值P_A/D与实际功率值P_W，然后用最小二乘法进行直线拟合得到一条P A/D和P W之间关系直线：

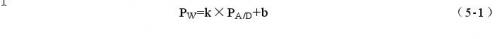
5.2.3频率校准部分

频率校准部分主要是校准温度对频率的影响。在前面硬件部分讲述过，温度对频率的影响主要是因为晶振的频率受到温度的影响，从而导致1秒门与实际有偏差。温度的校准也就是对门控的校准。校准程序主要通过查表的方式对门控的温度误差进行补偿。通过试验测得一组温度点和门控误差对应的数据。读取温度传感器读取当前温度的环境温度，查表获得对应点的门控误差。在温度点之间的温度值通过曲线拟合的直线获得此刻温度的门控的误差。将门控误差补偿后，

其中，freu为温度补偿前的频率值，T d为温度补偿后的门控信号。则fre为补偿后的实际频率。

5.2.4功率频响校准

功率的频响进行校准是功率校准主要部分。在设计中，以脉冲作为门控，对载波