射频中功率量值准确测量的研究

一、引言

随着通信、广播电视行业的飞速发展，对射频中功率的准确测量的要求越来越高，尤其是对发射机测试，基本都是要求在现场测试。对射频中功率测试的最简单的方法是采用功率计法，但测量不确定度只能达到8%~ 10% ，有时无法满足要求。为此，我们采用大功率衰减器和小功率计组合完成射频中功率的测量，测量不确定度达到了5% ，能够满足目前多数射频中功率测量的要求。

二、方案选择

我们选择Weinschel Crop.的大功率衰减器40-40-43和R/S公司的功率计NRVS组成这套测量系统。大功率衰减器40-40-43是一个40dB、最大连续波输入150W，工作频率范围DC~ 1.5GHz的固定衰减器，功率计NRVS的测量范围是10MHz~ 18GHz、1nW~20mW.整个装置设计的测量范围为频率:10MHz~ 1GHz、功率： ＜50W.

1.测量原理

该方法测量的原理如图1所示。

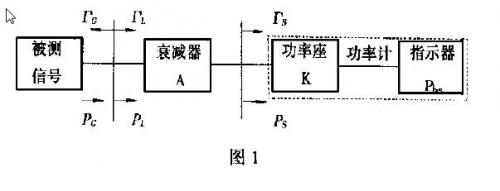
图中：

PS为小功率座吸收的净功率；

P_L为大功率衰减器输入端吸收的净功率；

P_G0为被测信号源连接无反射负载时的输出功率；

Γ_S为小功率座输入端的反射系数；

Γ_L为衰减器输入端的反射系数；

Γ_G为被测信号源输出端的反射系数。

将衰减器作为二端口网络，可得到被测信号的无反射负载输出功率P_G0表示式如下：

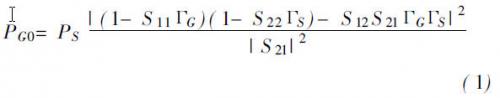
式中S₁₁、S₁₂、S₂₁、S₂₂是衰减器的四个散射参数。

根据衰减的定义可知：

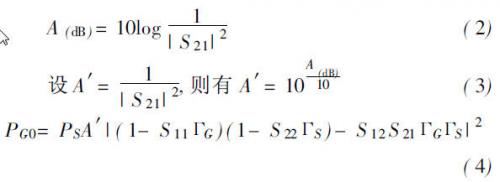
上式中失配项用M表示，即

式（ 4）改写

为设P_bS为小功率计的直流（或音频）替代功率， K为小功率座的校准因子。则净功率P_S可用下式表示：

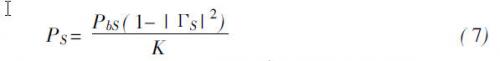
可见，已知衰减器的衰减量A′和小功率座的校准因子K ，就可由替代功率P_bS求得功率P_G0，

2.测量方案

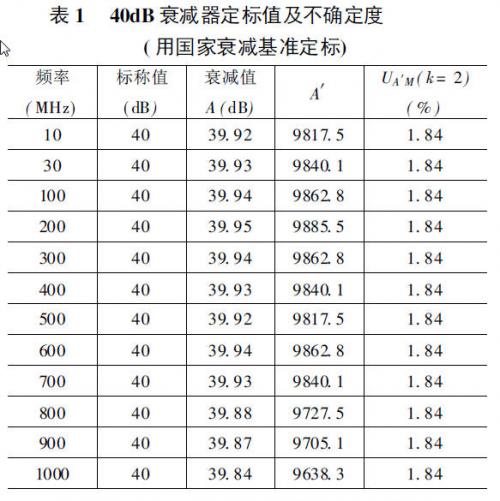
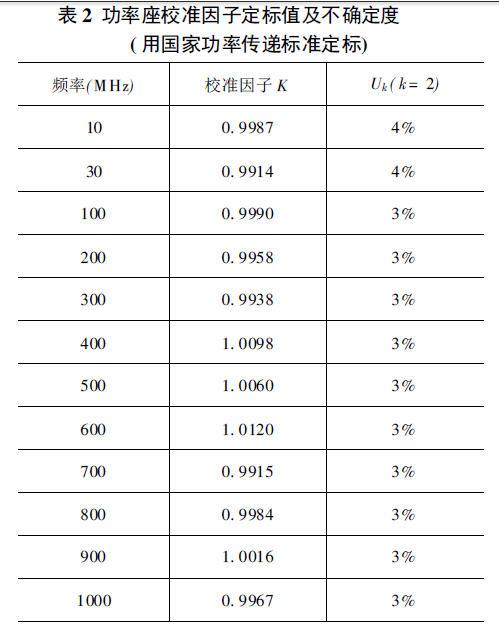
本测量系统中的衰减器和功率计定标值如表1、表2所示，其中U_A′M是衰减器定标值的扩展不确定度，U_K是功率座校准因子定标值的扩展不确定度。

3.不确定度分析

考虑到衰减器的衰减量会随输入功率的变化而变化，用衰减基准对其定标时，是在小功率信号输入时进行测量的，而在实际测量中输入的是大功率信号，因此必须考虑它给测量结果带来的不确定度。

Weinschel公司给出了大功率衰减器40-40-43在使用时功率对衰减量值的影响关系，如下式所示：

ΔA＜0.0001A·P （ dB） （ 8）

式中ΔA是衰减器的衰减变化量： A是衰减器的衰减量： P衰减器的输入功率的大小，由公式计算可得，在40dB，50W的使用情况下，衰减变化量小于0.2dB.

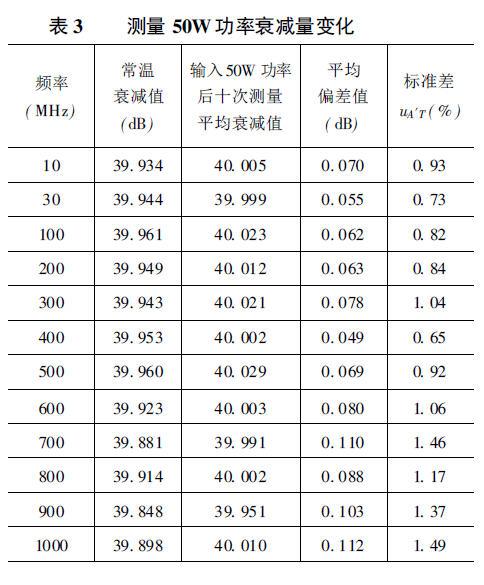
考虑到厂家给出的衰减量变化比较保守，同时衰减量变化随着通过功率的增大而增大，我们对衰减器在常温下和长时间通过50W功率信号后的衰减量分别进行了测量。

表3是应用网络分析仪测量在常温下和通过50W功率后衰减器的衰减值。表中U_A′T是由于50W输入功率引起的A′标准不确定度，假定其服从均匀分布。

由前面分析可得， PG0测量不确定度用式（7）计算式中：

uP为P_G0测量结果的标准不确定度；U_A′M为高功率衰减器定标值的标准不确定度； U_A′T为高功率衰减器测量大功率信号时衰减变化的标准不确定度；uS为P_S测量值的标准不确定度； u_M为系统失配的标准不确定度。

对于NRVS小功率计，其P_S测量值的标准不确定度由式（ 10）表示，具体数值见表2.

式中： u_Pbs为小功率座直流替代功率的标准不确定度，对NRVS小功率计＜0.3%； u_K为小功率座校准因子的标准不确定度。

衰减器的标准不确定度包括两部分，一部分是衰减器在常温下的标准不确定度，见表1中所示；另一部分是在进行大功率测量时，衰减器由于输入大功率信号后温度上升引起的衰减量的不确定度，这部分数据见表3中所示。

失配引起的不确定度由式（11）计算

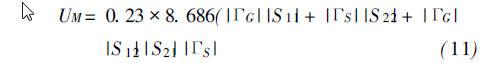
式中：ΓG = 0.3为被测信号反射系数； ΓS = 0.02为小功率座输入端的反射系数； S₁₁＜0. 0050为输入反射系数； S₁₂ ≈0.01为反向传输系数； S₂₁ ≈0.01为正向传输系数； S₂₂＜0.005为输出反射系数。

按式（11）计算可得： U_M ＜0. 32%对于U_A′M ，由于（k= 2） ，则u_A′M =U_A′M/ 2.详细数据见表1.对于U_S ，由于（k= 2） ，则u_S = U_S / 2.详细数据见表2.对于u_A′T，详细数据见表3.对于U_M ，由于（ k= √2） ，则u_M = U_M / 2.

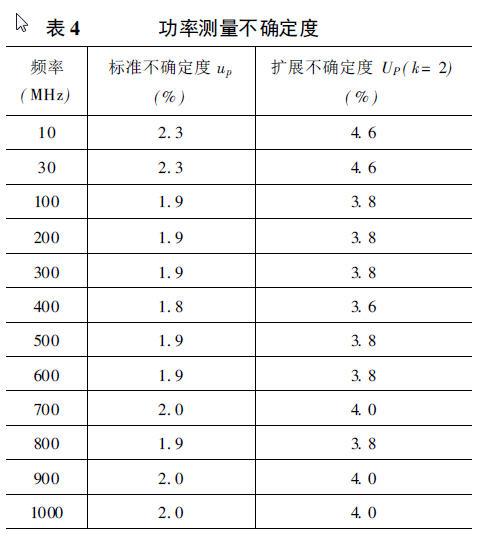
按式（ 9）计算，可得功率测量的标准不确定度u_p见表4所示。取k= 2，置信水准95%，其扩展不确定度U_P见表4所示。

三、结论

经测量和不确定度分析，该装置测量不确定度小于5%.是一种比较好的解决射频中功率量值准确测量的方法。