第39章 IIR滤波器的Matlab设计
本章节讲解IIR滤波器的Matlab设计,主要包括巴特沃斯滤波器,切比雪夫I型和II型滤波器以及椭圆滤波器。
39.1 巴特沃斯滤波器的设计
39.2 切比雪夫滤波器的设计
39.3 椭圆滤波器的设计
39.4 总结
39.1 巴特沃斯滤波器的设计
39.1.1 butter函数
39.1.2 buttord函数

39.1.3 巴特沃斯低通滤波器设计
下面我们通过一个实例来讲解巴特沃斯低通滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成,将200Hz的正弦波当做噪声滤掉,下面通过函数butter设计一组低通滤波器系数,其阶数是2,截止频率为0.25(也就是125Hz),采样率1Kbps。Matlab运行代码如下:
- fs=1000; %设置采样频率 1k
- N=1024; %采样点数
- n=0:N-1;
- t=0:1/fs:1-1/fs; %时间序列
- f=n*fs/N; %频率序列
-
- x1=sin(2*pi*50*t); %信号
- x2=sin(2*pi*200*t); %噪声
- x=x1+x2; %信号混合
-
- subplot(221);
- plot(t,x); %绘制原始信号
- xlabel('时间');
- ylabel('幅值');
- title('原始信号');
- grid on;
-
- subplot(222);
- y=fft(x,N); %绘制原始信号的幅频响应
- plot(f,abs(y));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('原始信号FFT');
- grid on;
-
- subplot(223);
- Wc=2*125/fs; %设置截止频率125Hz
- [b,a]=butter(2,Wc); %获取2阶IIR滤波系数
- % y2=filter(b,a,x);
- y2=filtfilt(b,a,x); %计算滤波后的波形y2
- y3=fft(y2,N); %滤波后波形的幅频响应
- plot(f,abs(y3));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('滤波后信号FFT');
- grid on;
-
- [H,F]=freqz(b,a,512);
- subplot(224);
- plot(F/pi,abs(H));
- xlabel('归一化频率'); %绘制绝对幅频响应
- ylabel('幅度');
- Ps=sum(x1.^2); %信号的总功率
- Pu=sum((y2-x1).^2); %剩余噪声的功率
- SNR=10*log10(Ps/Pu); %信噪比
- title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
- grid on;
运算Malab结果如下:
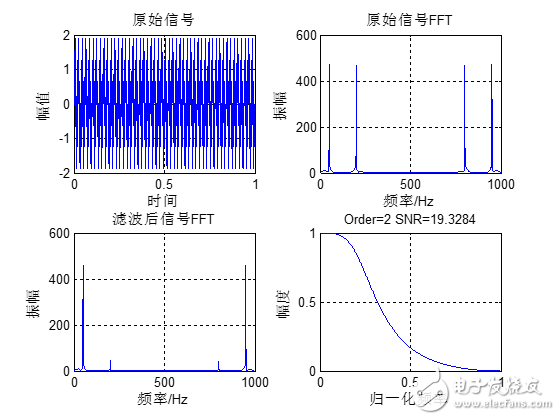
从滤波的效果来看,2阶的IIR滤波器能够达到将近20的信噪比,比使用FIR需要更少的阶数。
39.1.4 巴特沃斯高通滤波器设计下面我们通过一个实例来讲解巴特沃斯高通滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成,将50Hz的正弦波当做噪声滤掉,下面通过函数butter设计一组高通滤波器系数,其阶数是2,截止频率为0.25(也就是125Hz),采样率1Kbps。Matlab运行代码如下:
- fs=1000; %设置采样频率 1k
- N=1024; %采样点数
- n=0:N-1;
- t=0:1/fs:1-1/fs; %时间序列
- f=n*fs/N; %频率序列
-
- x1=sin(2*pi*50*t); %噪声
- x2=sin(2*pi*200*t); %信号
- x=x1+x2; %信号混合
-
- subplot(221);
- plot(t,x); %绘制原始信号
- xlabel('时间');
- ylabel('幅值');
- title('原始信号');
- grid on;
-
- subplot(222);
- y=fft(x,N); %绘制原始信号的幅频响应
- plot(f,abs(y));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('原始信号FFT');
- grid on;
-
- subplot(223);
- Wc=2*125/fs; %设置截止频率125Hz
- [b,a]=butter(2,Wc, 'high'); %获取2阶IIR滤波系数
- % y2=filter(b,a,x);
- y2=filtfilt(b,a,x); %计算滤波后的波形y2
- y3=fft(y2,N); %滤波后波形的幅频响应
- plot(f,abs(y3));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('滤波后信号FFT');
- grid on;
-
- [H,F]=freqz(b,a,512);
- subplot(224);
- plot(F/pi,abs(H));
- xlabel('归一化频率'); %绘制绝对幅频响应
- ylabel('幅度');
- Ps=sum(x2.^2); %信号的总功率
- Pu=sum((y2-x2).^2); %剩余噪声的功率
- SNR=10*log10(Ps/Pu); %信噪比
- title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
- grid on;
Matlab运行结果如下:
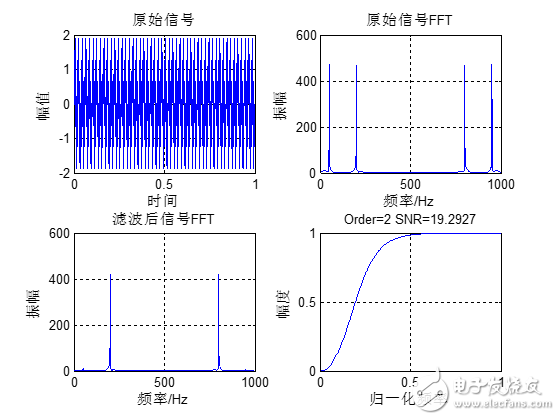
从滤波的效果来看,2阶的IIR滤波器效果还是比较好的。
39.1.5 巴特沃斯带通滤波器设计下面我们通过一个实例来讲解巴特沃斯带通滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成,将50Hz的正弦波当做噪声滤掉,下面通过函数butter设计一组带通滤波器系数,其阶数是2,通带为125Hz到300Hz,采样率1Kbps。Matlab运行代码如下:
- fs=1000; %设置采样频率 1k
- N=1024; %采样点数
- n=0:N-1;
- t=0:1/fs:1-1/fs; %时间序列
- f=n*fs/N; %频率序列
-
- x1=sin(2*pi*50*t); %噪声
- x2=sin(2*pi*200*t); %信号
- x=x1+x2; %信号混合
-
- subplot(221);
- plot(t,x); %绘制原始信号
- xlabel('时间');
- ylabel('幅值');
- title('原始信号');
- grid on;
-
- subplot(222);
- y=fft(x,N); %绘制原始信号的幅频响应
- plot(f,abs(y));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('原始信号FFT');
- grid on;
-
- subplot(223);
- Wn=[125*2 300*2]/fs; %设置通带125Hz到300Hz
- [b,a]=butter(1,Wn); %注意第一个参数虽然是1,但生成的却是2阶IIR滤波器系数
- % y2=filter(b,a,x);
- y2=filtfilt(b,a,x); %计算滤波后的波形y2
- y3=fft(y2,N); %滤波后波形的幅频响应
- plot(f,abs(y3));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('滤波后信号FFT');
- grid on;
-
- [H,F]=freqz(b,a,512);
- subplot(224);
- plot(F/pi,abs(H));
- xlabel('归一化频率'); %绘制绝对幅频响应
- ylabel('幅度');
- Ps=sum(x2.^2); %信号的总功率
- Pu=sum((y2-x2).^2); %剩余噪声的功率
- SNR=10*log10(Ps/Pu); %信噪比
- title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
- grid on;
Matlab的计算结果如下:

从滤波的效果来看,2阶的IIR滤波器效果还是比较好的。
39.1.6 巴特沃斯带阻滤波器设计下面我们通过一个实例来讲解巴特沃斯带阻滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成,将200Hz的正弦波当做噪声滤掉,下面通过函数butter设计一组带阻滤波器系数,其阶数是2,阻带为125Hz到300Hz,采样率1Kbps。Matlab运行代码如下:
- fs=1000; %设置采样频率 1k
- N=1024; %采样点数
- n=0:N-1;
- t=0:1/fs:1-1/fs; %时间序列
- f=n*fs/N; %频率序列
-
- x1=sin(2*pi*50*t); %信号
- x2=sin(2*pi*200*t); %噪声
- x=x1+x2; %信号混合
-
- subplot(221);
- plot(t,x); %绘制原始信号
- xlabel('时间');
- ylabel('幅值');
- title('原始信号');
- grid on;
-
- subplot(222);
- y=fft(x,N); %绘制原始信号的幅频响应
- plot(f,abs(y));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('原始信号FFT');
- grid on;
-
- subplot(223);
- Wn=[125*2 300*2]/fs; %设置阻带125Hz到300Hz
- [b,a]=butter(1,Wn, 'stop'); %注意第一个参数虽然是1,但生成的却是2阶IIR滤波器系数
- % y2=filter(b,a,x);
- y2=filtfilt(b,a,x); %计算滤波后的波形y2
- y3=fft(y2,N); %滤波后波形的幅频响应
- plot(f,abs(y3));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('滤波后信号FFT');
- grid on;
-
- [H,F]=freqz(b,a,512);
- subplot(224);
- plot(F/pi,abs(H));
- xlabel('归一化频率'); %绘制绝对幅频响应
- ylabel('幅度');
- Ps=sum(x1.^2); %信号的总功率
- Pu=sum((y2-x1).^2); %剩余噪声的功率
- SNR=10*log10(Ps/Pu); %信噪比
- title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
- grid on;
Maltab运行结果如下:
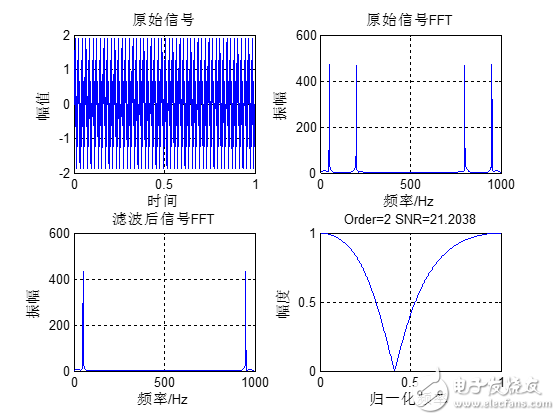
从滤波的效果来看,2阶的IIR滤波器效果还是比较好的。
39.2 切比雪夫滤波器的设计
切比雪夫(Chebyshev)滤波器分为Chebyshev I型和Chebyshev II型,分别具有通带等纹波和阻带等纹波性能。
39.2.1 cheby1函数
39.2.2 cheby1ord函数

39.2.3 cheby2函数

39.2.4 cheby2ord函数

39.2.5 切比雪夫I型低通滤波器设计
下面我们通过一个实例来讲解切比雪夫I型低通滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成,将200Hz的正弦波当做噪声滤掉,下面通过函数cheby1设计一组低通滤波器系数,其阶数是4,截止频率为0.25(也就是125Hz),采样率1Kbps,通带波纹1db。Matlab运行代码如下:
- fs=1000; %设置采样频率 1k
- N=1024; %采样点数
- n=0:N-1;
- t=0:1/fs:1-1/fs; %时间序列
- f=n*fs/N; %频率序列
-
- x1=sin(2*pi*50*t); %信号
- x2=sin(2*pi*200*t); %噪声
- x=x1+x2; %信号混合
-
- subplot(221);
- plot(t,x); %绘制原始信号
- xlabel('时间');
- ylabel('幅值');
- title('原始信号');
- grid on;
-
- subplot(222);
- y=fft(x,N); %绘制原始信号的幅频响应
- plot(f,abs(y));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('原始信号FFT');
- grid on;
-
- subplot(223);
- Wc=2*125/fs; %设置截止频率125Hz
- [b,a]=cheby1(4, 3, Wc); %获取2阶IIR滤波系数
- % y2=filter(b,a,x);
- y2=filtfilt(b,a,x); %计算滤波后的波形y2
- y3=fft(y2,N); %滤波后波形的幅频响应
- plot(f,abs(y3));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('滤波后信号FFT');
- grid on;
-
- [H,F]=freqz(b,a,512);
- subplot(224);
- plot(F/pi,abs(H));
- xlabel('归一化频率'); %绘制绝对幅频响应
- ylabel('幅度');
- Ps=sum(x1.^2); %信号的总功率
- Pu=sum((y2-x1).^2); %剩余噪声的功率
- SNR=10*log10(Ps/Pu); %信噪比
- title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
- grid on;
Matlab计算结果如下:
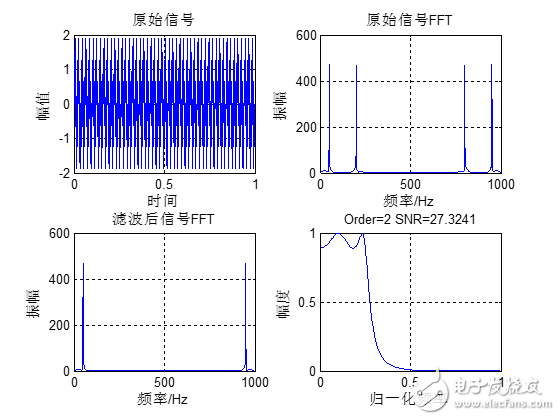
从滤波的效果来看,4阶的切比雪夫I型滤波效果还是比较好的。
39.2.6 切比雪夫I型高通滤波器设计
下面我们通过一个实例来讲解切比雪夫I型高通滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成,将50Hz的正弦波当做噪声滤掉,下面通过函数cheby1设计一组高通滤波器系数,其阶数是2,截止频率为0.25(也就是125Hz),采样率1Kbps,通带波纹1db。Matlab运行代码如下:
- fs=1000; %设置采样频率 1k
- N=1024; %采样点数
- n=0:N-1;
- t=0:1/fs:1-1/fs; %时间序列
- f=n*fs/N; %频率序列
-
- x1=sin(2*pi*50*t); %噪声
- x2=sin(2*pi*200*t); %信号
- x=x1+x2; %信号混合
-
- subplot(221);
- plot(t,x); %绘制原始信号
- xlabel('时间');
- ylabel('幅值');
- title('原始信号');
- grid on;
-
- subplot(222);
- y=fft(x,N); %绘制原始信号的幅频响应
- plot(f,abs(y));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('原始信号FFT');
- grid on;
-
- subplot(223);
- Wc=2*125/fs; %设置截止频率125Hz
- [b,a]=cheby1(2, 1, Wc, 'high'); %获取2阶IIR滤波系数
- % y2=filter(b,a,x);
- y2=filtfilt(b,a,x); %计算滤波后的波形y2
- y3=fft(y2,N); %滤波后波形的幅频响应
- plot(f,abs(y3));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('滤波后信号FFT');
- grid on;
-
- [H,F]=freqz(b,a,512);
- subplot(224);
- plot(F/pi,abs(H));
- xlabel('归一化频率'); %绘制绝对幅频响应
- ylabel('幅度');
- Ps=sum(x2.^2); %信号的总功率
- Pu=sum((y2-x2).^2); %剩余噪声的功率
- SNR=10*log10(Ps/Pu); %信噪比
- title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
- grid on;
Matlab运行结果如下:
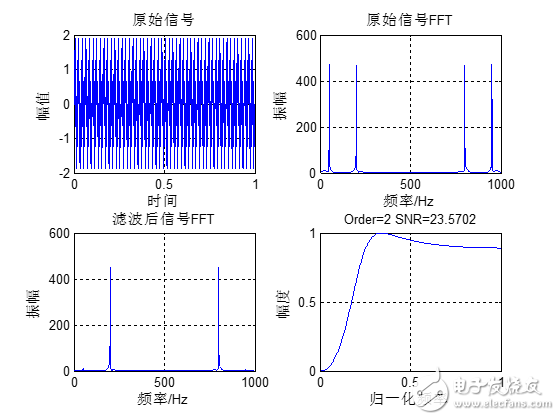
39.2.7 切比雪夫I型带通滤波器设计
下面我们通过一个实例来讲解切比雪夫I型带通滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成,将50Hz的正弦波当做噪声滤掉,下面通过函数cheby1设计一组带通滤波器系数,其阶数是2,通带为125Hz到300Hz,采样率1Kbps,通带纹波1db。Matlab运行代码如下:
- fs=1000; %设置采样频率 1k
- N=1024; %采样点数
- n=0:N-1;
- t=0:1/fs:1-1/fs; %时间序列
- f=n*fs/N; %频率序列
-
- x1=sin(2*pi*50*t); %噪声
- x2=sin(2*pi*200*t); %信号
- x=x1+x2; %信号混合
-
- subplot(221);
- plot(t,x); %绘制原始信号
- xlabel('时间');
- ylabel('幅值');
- title('原始信号');
- grid on;
-
- subplot(222);
- y=fft(x,N); %绘制原始信号的幅频响应
- plot(f,abs(y));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('原始信号FFT');
- grid on;
-
- subplot(223);
- Wn=[125*2 300*2]/fs; %设置通带125Hz到300Hz
- [b,a]=cheby1(1,1,Wn); %注意第一个参数虽然是1,但生成的却是2阶IIR滤波器系数
- % y2=filter(b,a,x);
- y2=filtfilt(b,a,x); %计算滤波后的波形y2
- y3=fft(y2,N); %滤波后波形的幅频响应
- plot(f,abs(y3));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('滤波后信号FFT');
- grid on;
-
- [H,F]=freqz(b,a,512);
- subplot(224);
- plot(F/pi,abs(H));
- xlabel('归一化频率'); %绘制绝对幅频响应
- ylabel('幅度');
- Ps=sum(x2.^2); %信号的总功率
- Pu=sum((y2-x2).^2); %剩余噪声的功率
- SNR=10*log10(Ps/Pu); %信噪比
- title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
- grid on;
Matlab的计算结果如下:

从滤波的效果来看,2阶的带通滤波器效果不够好,出现这种情况的时候,需要大家去重新的调节截止频率,滤波器阶数和通带波纹。
39.2.8 切比雪夫I型带阻滤波器设计
下面我们通过一个实例来讲解切比雪夫I型带阻滤波器的设计。原始信号是由50Hz正弦波和200Hz的正弦波组成,将200Hz的正弦波当做噪声滤掉,下面通过函数cheby1设计一组带阻滤波器系数,其阶数是2,阻带为125Hz到300Hz,采样率1Kbps,通带波纹1db。Matlab运行代码如下:
- fs=1000; %设置采样频率 1k
- N=1024; %采样点数
- n=0:N-1;
- t=0:1/fs:1-1/fs; %时间序列
- f=n*fs/N; %频率序列
-
- x1=sin(2*pi*50*t); %信号
- x2=sin(2*pi*200*t); %噪声
- x=x1+x2; %信号混合
-
- subplot(221);
- plot(t,x); %绘制原始信号
- xlabel('时间');
- ylabel('幅值');
- title('原始信号');
- grid on;
-
- subplot(222);
- y=fft(x,N); %绘制原始信号的幅频响应
- plot(f,abs(y));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('原始信号FFT');
- grid on;
-
- subplot(223);
- Wn=[125*2 300*2]/fs; %设置阻带125Hz到300Hz
- [b,a]=cheby1(1,1,Wn, 'stop'); %注意第一个参数虽然是1,但生成的却是2阶IIR滤波器系数
- % y2=filter(b,a,x);
- y2=filtfilt(b,a,x); %计算滤波后的波形y2
- y3=fft(y2,N); %滤波后波形的幅频响应
- plot(f,abs(y3));
- xlabel('频率/Hz');
- ylabel('振幅');
- title('滤波后信号FFT');
- grid on;
-
- [H,F]=freqz(b,a,512);
- subplot(224);
- plot(F/pi,abs(H));
- xlabel('归一化频率'); %绘制绝对幅频响应
- ylabel('幅度');
- Ps=sum(x1.^2); %信号的总功率
- Pu=sum((y2-x1).^2); %剩余噪声的功率
- SNR=10*log10(Ps/Pu); %信噪比
- title(['Order=',int2str(2), ' SNR=',num2str(SNR)]);
- grid on;
Matlab计算结果如下:
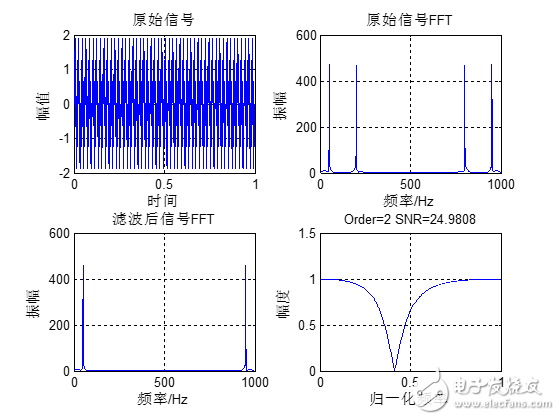
从滤波的效果来看,2阶带阻滤波的效果较好。
39.3 椭圆滤波器的设计
39.3.1 ellip函数


关于椭圆滤波器的使用,大家参考前面的切比雪夫滤波器设计即可,使用方法基本是类似的。但是由于椭圆滤波器要同时给我通带和阻带的纹波,所以要得到满足要求的滤波器系数要花些时间去做测试。
39.4 总结
本章节主要讲解了巴特沃斯,切比雪夫和椭圆滤波器的设计,如果想用好还需要大家多多做测试,并深入了解相关理论知识。
好东西,值得一看。
