Phase and attenuation constant 1-D periodic structure using CST or HFSS
I intend to plot B/ko and a/ko plots of this paper through simulation either in CST or HFSS. The plots are shown in figure 5 of the paper (link below). The link to implementation of this antenna in CST is below as well. I have come across alot of answers but none of them seem to give me the right plot and at this point, I am not sure which one of them is right. I have tried eigenmode solver using slow-wave example, frequency domain solver has a gamma plot but normalizing it through ko doesn't give the right response either. Also, I have plotted in HFSS using floquet ports. and I have tried to use the formula [acos(((1-s(1,1)*s(2,2)+s(1,2)*s(2,1)))/2/s(2,1)) ]. Please assist me on this. Thanks.
Paper: https://ieeexplore.ieee.org/stamp/st...number=8754760
Implementation of paper in CST: https://drive.google.com/drive/u/1/f...oWMtLg_KDUzjaj
Please convert your project files to a zip file. Upload as an Edaboard attachment.
That is preferable to making readers click multiple times to view all items at your Drive.google link.
Below is your zip file reworked so it contains only your cst project (94 KB). Post #1 still has the link to the research paper.
https://www.edaboard.com/attachment....5&d=1572235691
Make sure you are observing the correct mode; the authors in that papers state it's a microstrip mode that they're working with.
Floquet ports are for exciting plane-wave harmonics, not guided-wave modes.
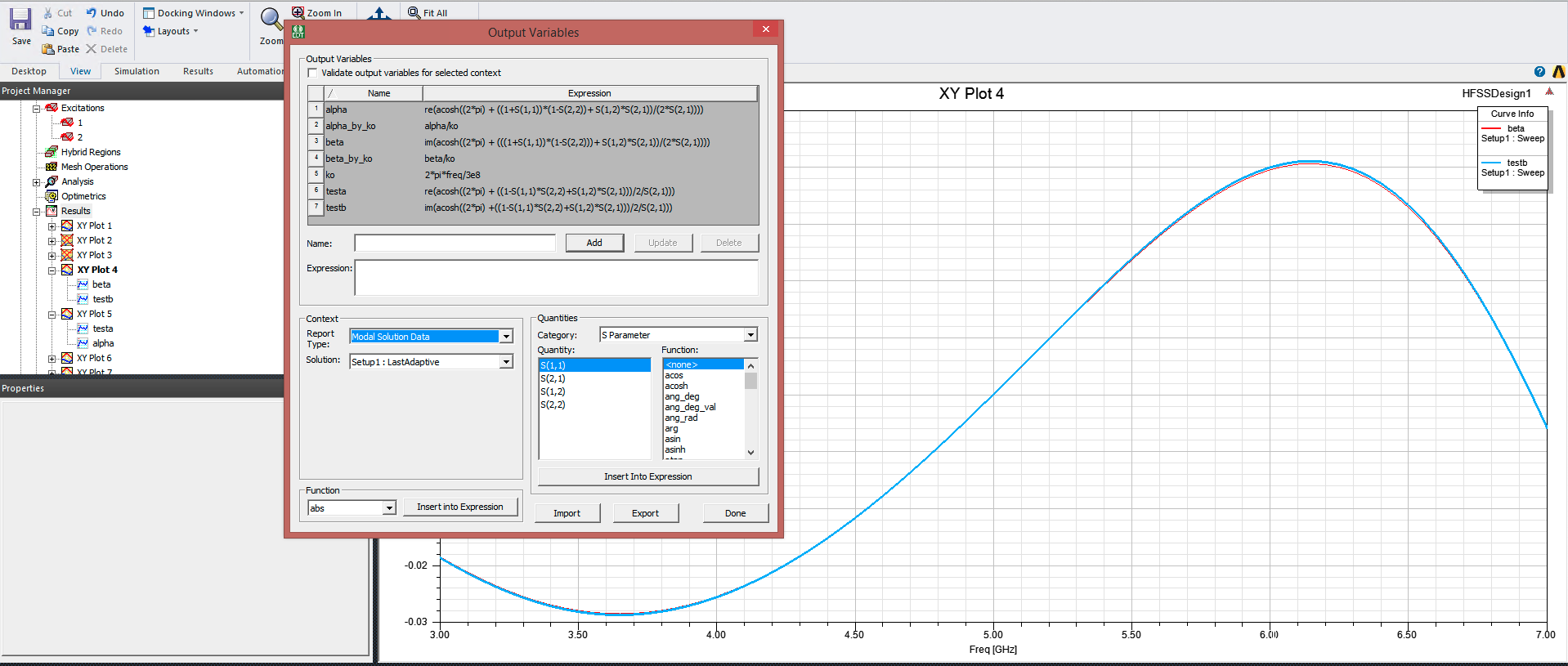
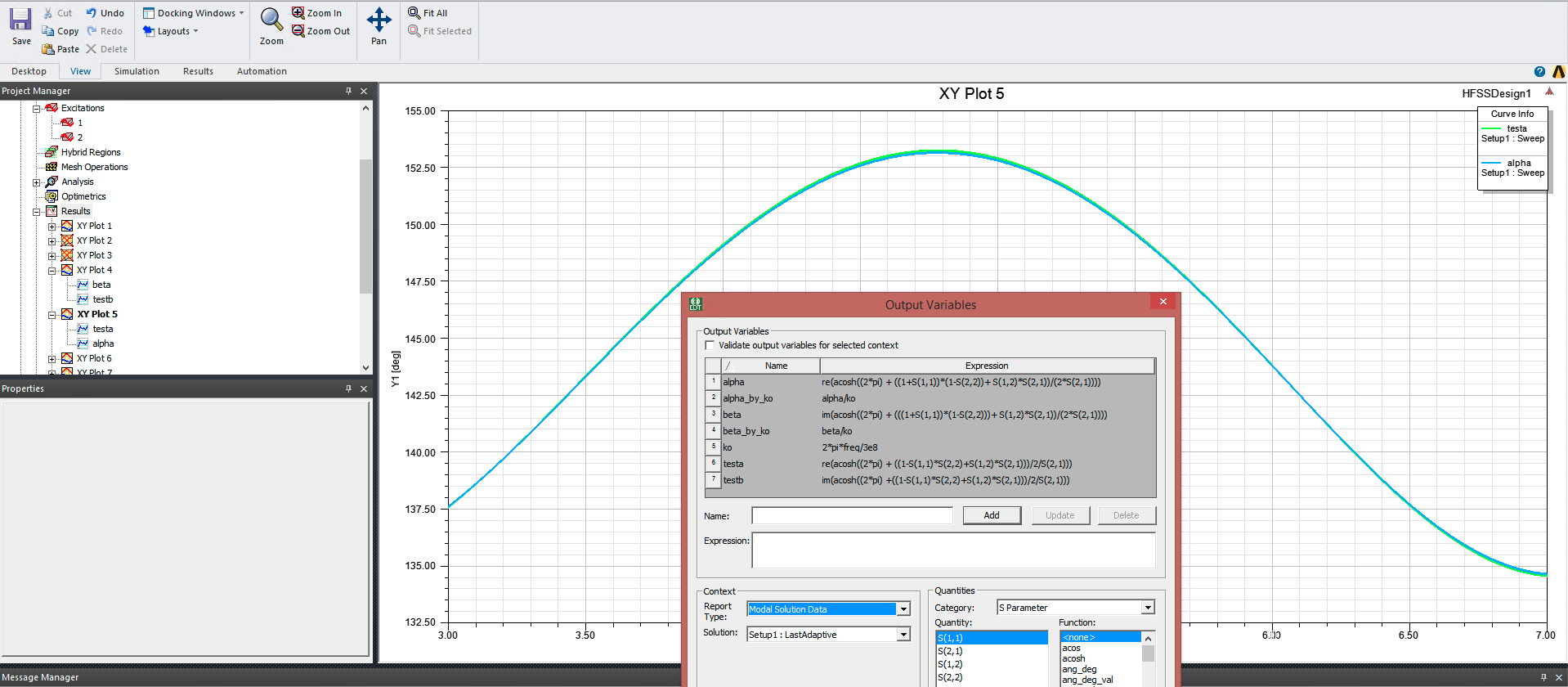
The equation is correct (using acosh instead of acos to find complex Gamma, and don't forget to divide by the period of the unit cell!), but you do need to consider branching: try adding some some various integer factors of n in of 2*pi*n, such that your equations should be:
acosh((2*pi*n) + ((1-s(1,1)*s(2,2)+s(1,2)*s(2,1)))/2/s(2,1))/d
Good luck!
I've plotted the results here for n = 1; they look like the results you want (I didn't include the period d or convert from degrees to radians).