problem: coupling coefficient for two hairpin resonators

hi
i want to find the coupling coefficient of two hairpin resonators with this configuration:

but I'm not getting two resonant peaks to calculate the coupling coefficient:

i don't know what's wrong. are the feeds placed correctly?

thanks

The Resonators are identical and if the coupling is tight, I think this is normal.
It looks like a coupled LC Resonators..

What Q's and coupling coefficient did your expect? Your equivalent BW= 125 MHz averaged at 2153 MHz (but asymm.) results in a Q of 17.

You may compute the Q from each outside skirt and then the coupling factor as said before with any double tuned coupled resonator equiv cct. depending on Q and spacing of f1,f2. The phase response may be more sensitive or accurate for this calc..

hi BigBoss
I want to redesign the results obtained by this paper:

kim2011.pdf

and I used the dimensions mentioned in the paper. this papers mentions 4 coupling coefficients between identical resonators which are placed in different directions and spacing with respect to each other. I am trying to extract the coupling coefficients mentioned in the paper. as I said the dimensions I chose, are the ones in the paper. if this structure can't show the coupling coefficient, how is it calculated in this paper?


hi SunnySkyguy
right now i am more concerned with the coupling coefficient to be able to design the poles and zeros of the filter. I'll try the phase response but i think there should be a way to calculate coupling coefficient by two peak resonances of the magnitude of S21.

Input and output ports must be very weakly coupled to the resonators.
See also examples in the book "Microstrip Filters for RF/Microwave" (Hong/Lancaster).

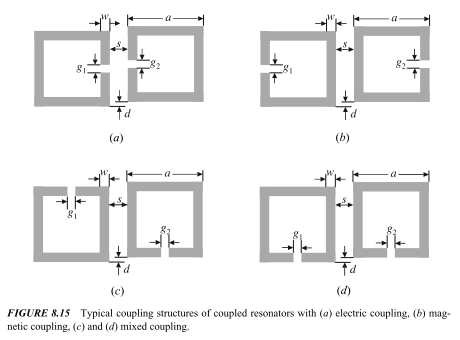
Hi niki

thanks for the advice about the resonators to be weakly coupled. I changed the feed positions and I got the two resonant peaks:

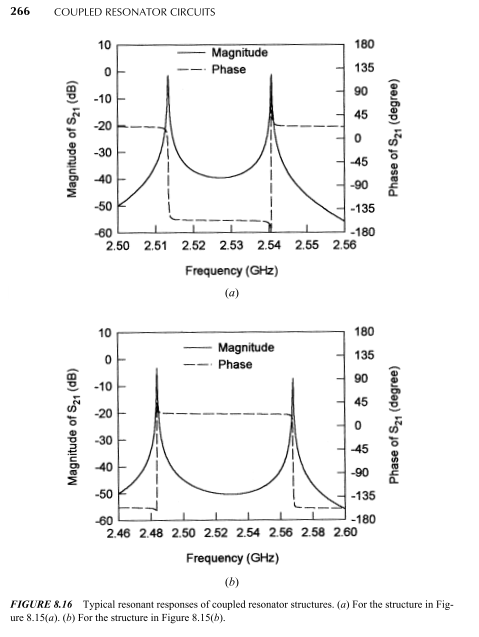
regarding the book you mentioned: I had seen this book and actually I was trying to obtain the same result which you showed here (figure 8.16). I used the values mentioned in the book, page 265:

this is how I placed the feed

which is similar to what was shown in the book:

and this is my simulation file:
lancaster_CH8_coupling_eda.rar

as you said i tried to weaken the coupling by moving the feed towards the center, as was mentioned in the book:

"... the coupling or the external quality factor is controlled by the tapping position t, the smaller the t, the weaker is the coupling coefficient ( or a larger external quality factor)..."

but this is what I get

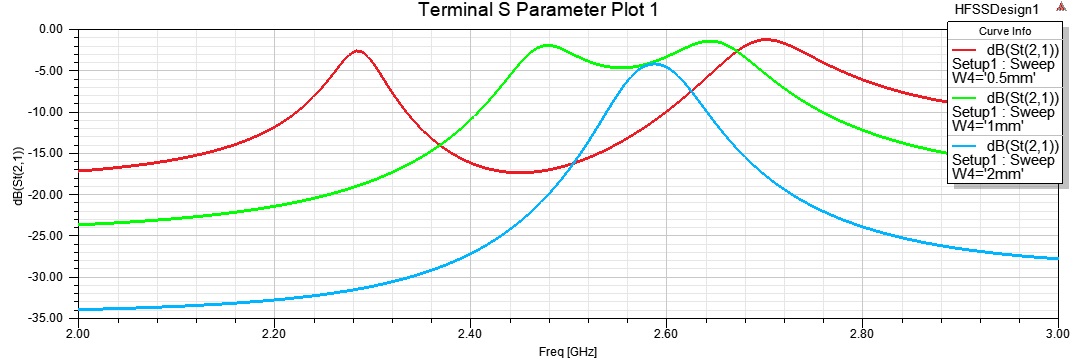
as you can see there is no coupling at S=2, and there is coupling for S=1mm and S=0.5 mm. I can't get the sharp peak shown in figure 8.16. any ideas ?

I guess there is something wrong with the feed again. should the width of the feed be less than the width of the open ring resonator?

Those are really high Q resonators. Maybe your conductor losses and/or substrate losses are too high, so that possible Q is too low.

I have simulated that resonator in AXIEM and found that the resonator coupling gap has reverse effect compare to standard ones.

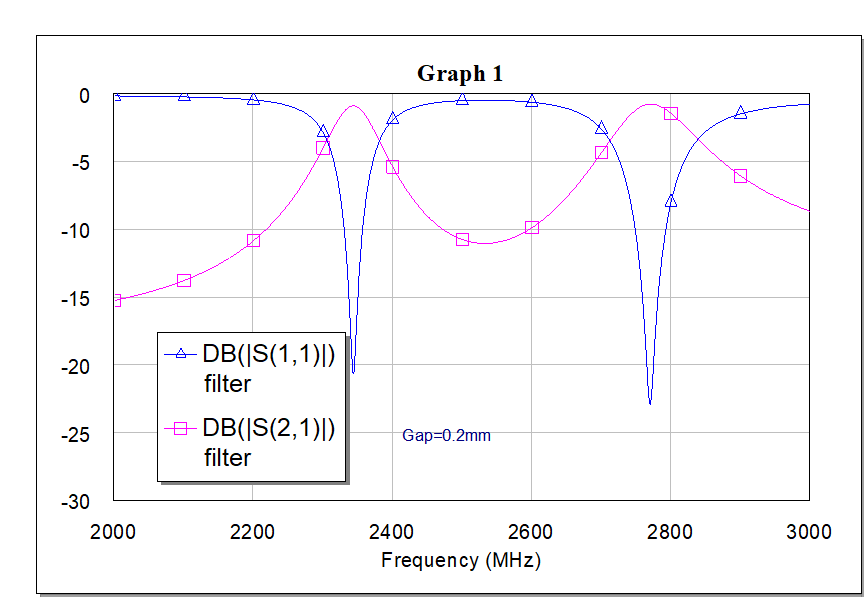
I used copper for conductors and other properties are those mentioned in the book. maybe the results shown in the book are for a slightly different structure. I'll try to set all losses to zero and see what will happen.




those results are fine. As you make the gap smaller, the peaks distance becomes larger which results in a larger coupling coefficient (the resonators have a greater effect on each other). but still your results are different from those of the book, both in magnitude and peak frequencies. so I am coming the conclusion that the results shown in figure 8.16 belong to a different but similar structure.

thanks for simulating the structure.

I think the results of that textbook in fig 8.16 are theoretical or analytical not EM simulated.Otherwise the peaks cannot be so sharp in practical world.