请教系统高手,环路稳定性的问题
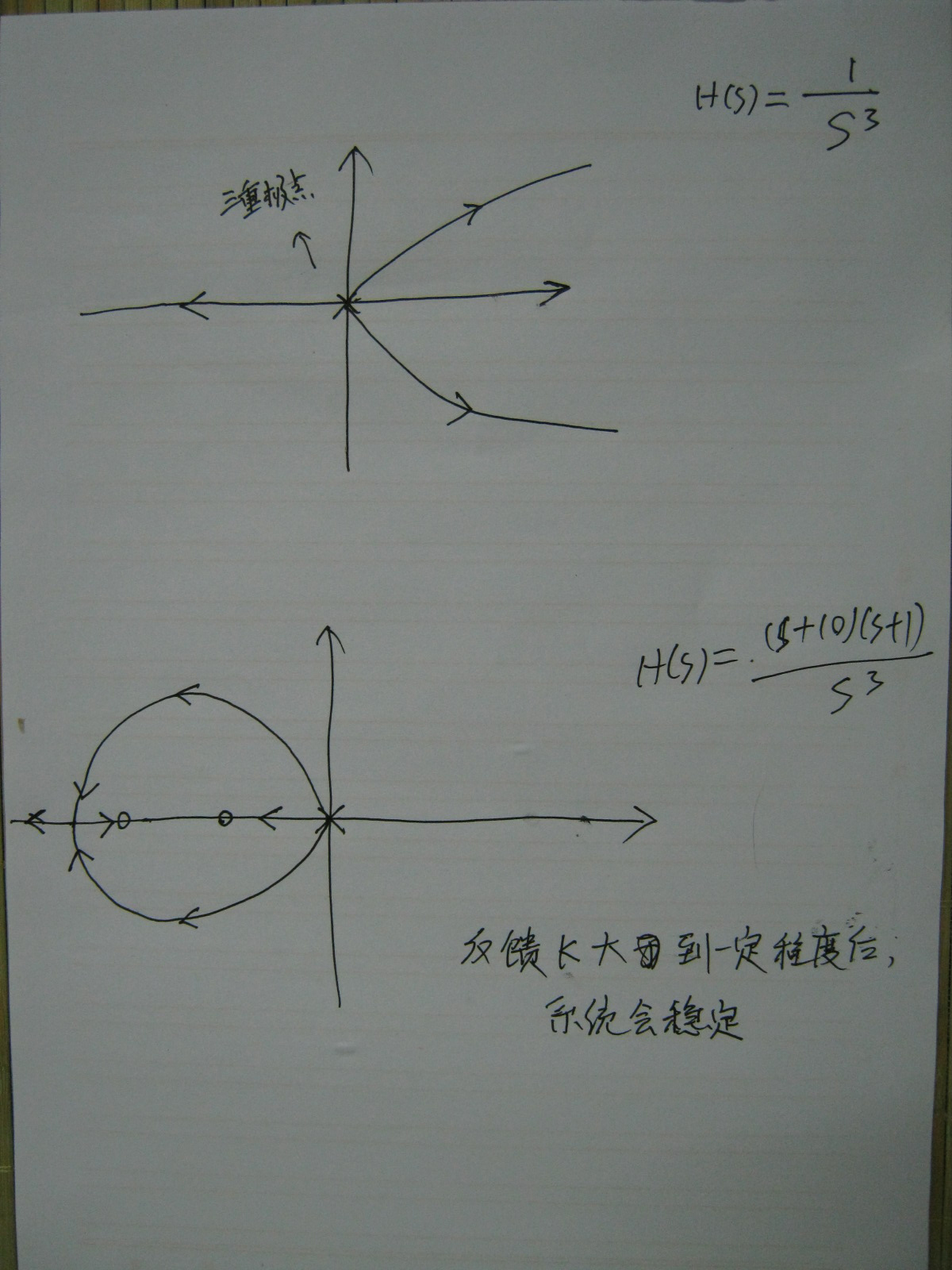
如果开环的传输函数是:A/s^3,
(s^3表示s的三次方,下同)
那么接成单位负反馈的形式, 环路能稳定吗?
如果是:
A(1+s)*(10+s)/s^3,
也接成单位负反馈的形式, 能稳定吗?
虽然结果我也知道,
但是感觉自己也是一知半解,
查阅了一些书籍,
感觉对这个问题没有很详细解答,
所以希望坛子里的高手能给予明示,
越详细越好,
能推荐书籍,资料也非常好,
不胜感激!
第一种:肯定不稳定,原点处有3个极点。
第二种,肯定不稳定,原点处有3个极点。
画出根轨迹图,第一种肯定不稳定,而且会有增幅振荡
第二种A值大到一定程度会稳定(闭环极点全跑到实轴上了),也就是说,随着A的增大,系统从减幅振荡到稳定
还可以通过画波特图来看相位裕度和稳定性
第一个函数基本没相位裕度
第二个函数增益够大的话,可以有90度的相位裕度
画根轨迹的方法信号与系统里面有,过程也比较简单。你也可以在matlab里面敲这个命令来画根轨迹图
%%%%%%%%%%%%% 绘画根轨迹 %%%%%%%%%%%%%%%%
num=[0 0 0 1];
den=[1 0 0 0];
rlocus(num,den);
%%%%%%%%%%%%% 绘画根轨迹 %%%%%%%%%%%%%%%%
num=[0 1 11 10];
den=[1000];
rlocus(num,den);
good reference , tKS fro sharing
第二个也不稳定吧?我感觉的,也不是很清楚。
第二个会有相移180度,增益大于1的情况。按说这样会震荡吧。
相位裕度只是必要条件,不是充要条件。
无论A怎样
第一个振荡
第二个可能振荡,取决于A的值。
--------------------
乃奎斯特图也能解释,只是画图也不容易
我还是觉得第二种会震荡。
我觉得稳定需要满足:相位裕度足够;增益裕度足够;没有满足震荡条件的点(相移180,增益>1)。
第二种电路满足不了第三个条件。相位裕度足够(假如为15度)也不行,因为相移从270降到165之前肯定会经过相移180度,而这时增益还没有降到小于1.
并不是相位裕度够就行了,没到带宽之前的点也可能震荡的。
欢迎拍砖
----------------
这种想法,从某些模拟电路教材来的吧
不知害了多少人啊
建议去看看自动控制方面的书,
否则,
如果被牛逼的公司不幸问到这个问题,直接把你PASS掉
到时后悔都来不及
用乃奎斯特曲线和理论能很好的解释这个问题了。
谢谢大家的跟帖!
楼上推荐一下资料看看,最好是网上的pdf。
我没书
分析的不错,还是得多看书
不解。
设计振荡器的时候不是要做到电路相移180度时增益大于1么?
难道第二种电路可以不过相移180度的点,而得到足够的相位裕度?
我承认我是从拉扎维的书上看的巴克豪森准则(P392,中文版)
全面的稳定性判据实这样的,
设开环右半平面实际点个数为P,
乃奎斯特曲面正穿越点(-1,0j)左侧实轴次数为N+,
乃奎斯特曲面负穿越点(-1,0j)左侧实轴次数为N-,
则稳定的充要条件是:
P-2(N+-N-)=0
抱歉我一点儿不懂根轨迹。
你能从我的角度证明一下没有满足我13#说的振荡器条件的点么?
或者证明下我所说的振荡器条件是错的?
相移180度的时候负反馈变正反馈,如果增益大于1,信号不断循环增加,是增幅振荡。错了么?
粗看了一眼,“奈奎斯特稳定判据的基本形式表明,如果系统开环传递函数G(s)在s复数平面的虚轴jω上既无极点又无零点,那么有 Z=P-2N ”
现在情况二是有三个极点在0。0是实轴和虚轴的焦点?算不算在虚轴jw上有极点?
如果算是虚轴上有极点,就不能用Z=P-2N公式了吧?
即使使用Z=P-2N。
P=3
只有一次正穿越
Z=1,不等于0,不稳定啊
我也觉得两种都不稳定,因为分母是S^3,而不是什么(S+0.1)^3或(S+0.0001)^3,也就是,在频率等于0处,开始产生相移,在频率等于0^3=0处,3个极点的相移达到270度,也就是增益还没有任何变化时,相移已经有270度,只要增益A>=1,这是不能稳定的,
而如果极点不在原点,哪怕是在任何接近原点的位置,比如0.001,相位都有1个从0下降到270度的过程,如果A取的合适,还有稳定的可能。
不知道这种分母是S^3的传输函数,在实际中存在吗?觉得很奇特,像这种分母是S^3或S^2的,做波特图,在f=0处,直接就是正反馈,只要开环增益不小于1,对于直流,一定不会稳定,而平时研究的反馈系统,在信号路径中,不管主极点多靠近原点,也不会就在原点上,也就是,相移是从0开始逐渐增加的。如果实际中有这样的传输函数,请指点,是在什么样的电路模型中呢?
原点处有3个极点
积分器的极点就在原点上,一个极点。
1/s,这是最常见的,gm+电容。
回楼上(20楼),谢谢!是的,理想的积分器模型是1/s,那是基于理想电流源输出阻抗无穷大的假设,想想实际中的交流情况,对于积分器的输出电压,极点位置是1/2*pi*Rout*C,Rout是充电电流镜的输出阻抗。无论你的C多么大,它也不会在原点上。
这和研究环路时的情况是一样的,我们很多情况op的输出也只有电容负载,但那个电容产生的极点也不在原点,而是在1/2*pi*Rout*C的位置,Rout是op的输出阻抗。是吧,呵呵,
估计还得好好学自动控制啊
有最终结果了么?第二种稳定还是不稳定?
现在分裂成两派了,一拨支持稳定,一拨支持不稳定。
我是不稳定那拨的。
是啊,这个题目说的就是理想情况。
mark,支持这种热烈的讨论氛围
一看到系统稳定性的东西就头晕,还是需要多看书了
小编解释的非常透彻!赞!
奎斯特图也能解释,只是画图也不容易
