说说 傅立叶变换 和 拉普拉斯变换(z 变换)

首先，可以把 拉普拉斯变换和z 变换（生成函数）视为一体，两者都是拉普拉斯提出的。
拉普拉斯作为傅立叶的导师，并不认同复立叶提出的 复立叶变换，直到拉普拉斯去世，傅立叶才正式发表，直到柯西提出了关于极限的严格收敛条件，傅立叶才放心大胆使用它的理论。
从历史的角度来讲，傅立叶变换出现在拉普拉斯变换之后，从形式上说，他们是类似的，但是出发点是不相同的。

拉普拉斯变换：拉普拉斯变换的基本思想其实是源于函数的幂级数分解。

对于因果系统的分析，拉普拉斯变换都是单边的，这点非常重要。

z变换（生成函数）一定程度上可以视为是函数幂级数展开的逆运算，也就是已知系数，求原函数，它是一个累加的形式。当把累加形式变成积分形式，就有了拉普拉斯变换。这是一个自然的过程， 这是也历史，当然最初的形式和信号分析中的形式也有区别。在信号处理中，则通常是先引入对信号的拉普拉斯变换，然后对此信号采样后再进行拉普拉斯变换，得到z变换。很多书本直接给出拉普拉斯变换的形式，其实应该有一些过渡。

傅立叶变换：傅立叶变换的基本思想源于正交分解。

复立叶级数一生下来时也是单边的，当引入复指数信号时，单边变成了双边。

如果说Laplace是从幂级数展开的思想发展出来的拉普拉斯变换，那么傅立叶更加有针对性地研究周期信号的三角级数展开（或者说是分解）。

拉普拉斯变换更多的是针对系统的分析和处理，主要是微分方程（差分方程），冲击响应，传递函数，零点极点和频率响应，稳定性分析。

傅立叶变换更多的是针对信号的分析和处理，主要是频谱分析。

仰望！

still confused

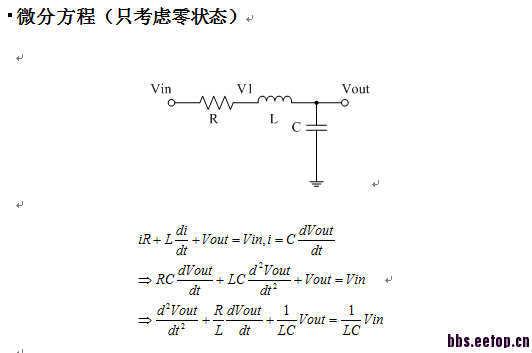
你可以考虑一下系统函数是怎么来的.
当然几乎每本书都有,只是我的推导方式跟书本不太一样.
没有复立叶变换，照样可以有系统函数，并且有一整套分析理论。这就是拉普拉斯变换的意义。
复立叶变换，也可以导出系统函数，运算形式更加简单漂亮。仅仅有复立叶变换，不会有零点极点这类概念，不利于从更高层次去分析系统。分析频谱 频响是复立叶的长项。
很多人，包括一些书本说 ， 拉式变换是 把复指数信号视为基本信号，把信号写成复指数信号的线性组合，从表达式上看，可以这么理解，但是我认为这种理解过于牵强。原因之一就是，复立叶变换正交分解的思想导致它以复指数信号为基信号时，是双边变换。硬把拉普拉斯变换视为对某些不收敛的信号乘一个衰减因子后的复立叶变换，其实没什么实际意义。（包换衰减因子）复指数信号严格来讲也不能作为基来存在，我个人是这么认为的
。
在线性系统中，微分方程（差分方程）是第一步，特征多项式是求解微分方程特征根（系统极点）的技巧，拉普拉斯变换是这一技巧的重要依托，而由此衍生出一整套（控制）理论。
复立叶变换，源于正交分解，用于拆分信号，求某组正交基下的坐标。顺带者也有微分特性，可以解微分方程。
把两者建立起联系不过是后人一厢情愿的事情罢了，因为他们长得实在太像了。

good, mark it ！

十分感谢，我再努力看看

完全看不懂的飘过。

拉普拉斯变换：http://www.fuzihao.org/blog/2014 ... %E4%BB%80%E4%B9%88/
这是MIT教授的观点，我认为很有启发性。最重要的性质就是线形性和微分特性。
复立叶变换：他的思想，简单地说就是把一个向量 投影到 三个坐标轴上。
学习信号系统会淹没在大量例题和公式中，要时不时地跳出来看看。

数字信号处理

牛人呀 膜拜……

仍旧头大。

thanks

膜拜， 还是不太理解 ：）

看透本质就懂了