PLL环路是否稳定的判定方法
那判断是否稳定,是看幅频曲线的增益在0dB时候,对应相频曲线频点处的相位裕度。
对于电荷泵型PLL,
我的问题是: 看增益下降到0dB的那一点的相位-(-180)=相位裕度,从而判断稳定性。
那么,在原点处,相位为-180,相位裕度为0,而增益确很大,这是否稳定呢?
此外,从原点到0dB点,有一大断都是相位为-180,相位裕度为0,而增益>1,这又是否稳定呢?
我的理解主要是从放大器的稳定性上推过来的,但是放大器稳定是不振荡,而PLL稳定是振荡在一个频率上,是否这上面有差别?
是否有朋友想过这个问题呢?
这个问题很有意思。
从放大器来说,假设放大器的开环增益特性与pll开环增益特性完全一样,就是在dc有相移180度增益还无穷大,那么完蛋了,构成负反馈闭环系统后肯定不能正常工作,不是振荡而是死锁,因为dc已经等效正反馈了。
pll环路确不会有这个问题。放大器反馈系统处理的物理量是电压,从dc开始的所有频率的电压信号。pll环路处理的却是相位误差或叫phase noise,有意思的是环路中各个节点的物理表现形式还不一样,在pfd输入端是检测两个clk的相位之差,cp输出的确是电流,lpf之后又变成了电压量并控制vco输出的频率。phase noise是一个dBc的概念,是频率偏离中心频率的抖动,可以理解为没有dc的信号。因此pll环路处理的是频率大于0的信号。负反馈系统中的稳定性理论是说:在频率响应带来的额外180度相移处增益仍大于1系统才不稳定。pll系统中没有dc信号,尽管传函说明在dc有180度相移,也不会不稳定。靠近dc的位置相移尽管接近180度,但只是无限靠近,也不会有稳定的问题。大于odB带宽之后,相移会穿越180度,但那时增益已经小于1,所以也是稳定的。
pll环路处理的是频率大于0的信号可以解释近端的相位裕度为0,而增益>1是合理的吗?
或者说,PLL处理相位差,而相位为-180度,变正反馈,经过放大,相位差变大,如此反复,PLL还是不会稳定的啊?
还是没有弄明白。
在一篇博文中http://blog.ednchina.com/yulzhu/267972/message.aspx
有说到,对-180度的正负穿越次数相差为0,再看相位裕度也是稳定的一种,不知是否适用。
总之,没有完全想明白!
对于一个二类三阶PLL来说
频率趋近于0,相位趋近180度,但是只要频率>0,相位永远不会达到180度,只是趋近。虽然phase margin很低,但是不会振荡。环路会有DC吗? DC意味着鉴相的相位差完全不随时间变化,会出现这种情况吗?实际上应该不会出现这种情况。所以不用担心稳定性。
但是对于二类4阶以上的PLL,相位会出现穿越180度的情况,高频区会有稳定性的问题;
谢谢楼上。
“频率趋近于0,相位趋近180度,但是只要频率>0,相位永远不会达到180度,只是趋近。“
这里的频率是理解为相位差对时间的变化率吗?
那么,对于0dB处的带宽Wc是如何理解的呢,是相位差随时间的变化范围?PLL的相位变化捕捉范围?
假设参考时钟是理想的sin波,相位不变,那么只要VCO频率范围满足要求,是否一定能锁定?
假设参考时钟是理想的sin波,相位变化率>Wc,那么即使VCO频率范围满足要求,一定不能锁定?
期待更多的人参与讨论!
PLL环路处理的信号是相位抖动,因此与环路相关的频率也是指相位差随时间变化在频域的反映,与vco振荡的中心频率没有关系。pll小信号模型中是没有reference频率和vco中心频率这两个参数的。
pll的工作原理本质上是利用环路对reference时钟抖动和对vco时钟抖动具有不同的传输函数。对前者是低通,对后者是高通。于是闭环vco最终的噪声特性在较低的频偏处(即pll 带内)表现为reference的噪声特性,在较高频偏处(即pll 带外)表现为开环vco噪声特性。
vco是否振荡在预期的频率上并不是判断锁定与不锁定的判断。vco振荡在预期的频率上并且噪声特性符合上面的描述才能判断环路是锁定的。
那将0dB处的带宽Wc理解PLL的相位变化捕捉范围对吗?
这个问题一直困惑我,感觉大家没有回答到真正的问题,请大家继续探讨,谢谢!
这个理解没错。但要注意捕捉相位变化包括两个方面:跟踪reference相位变化和抑制vco相位变化。
pll 开环增益0dB处表示:环路闭合后对reference相位变化失去跟踪能力,另一方面对vco的相位变化失去抑制能力!
实际应用中,reference相位噪声在pll带宽处是非常低的,一般在<0.1*pll带宽处reference相位噪声就已经达到噪底了,因此带宽处失去跟踪能力并没有关系。这就是为什么在选取带宽时,限制条件往往是vco的噪声水平,带宽必须足够宽以保证能对vco噪声有足够抑制。
但是没有回答稳定性的问题呀?
对的,只是频率大于零,一般的tpye 2 PLL都是稳点的,如果各位了解根轨迹对系统稳定性的判定方法,那么就可以很快得出结论。
请问楼上有介绍根轨迹对系统稳定性的判定方法的来龙去脉的资料吗?
我觉得随着问题的讨论,能够越来越清晰地了解PLL系统了。
真是问题不辨不明啊!
要是从开环的BODE图来看,DC附近的相位180度,系统会不稳定,大家还没有真正回答这个问题
已经回答了,没有DC。
DC附近,也不会=-180.
phase margin只是一个充分不必要条件吧,用自动控制原理里的稳定性判断比较容易吧
建议带上LF (loop filter)做PLL的open loop and close loop AC simulation
BODE图看稳定性是有适用范围的,是Nyquist原理在某种条件下的简化。
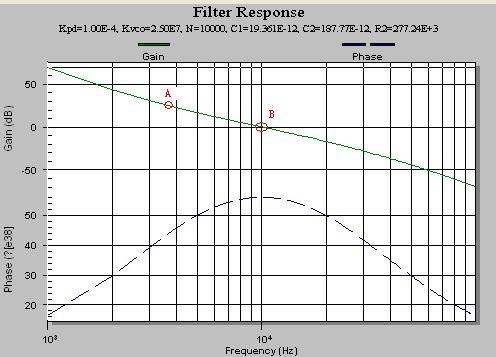
想了想,还是有点问题,如下图:一般会将幅频、相频图设置成下图所示,而关心的是B点的相位裕度。
问题是,相对于B点,A点增益>1,相位又比B点差,岂不是更不稳定的点?
与放大器区别在于,放大器的开环相频曲线相位是从-90向-180走的。而PLL开环相频曲线是从-180向-90走的。
放大器考查0dB点的相位裕度作为稳定性判据是想的通了,而PLL也这样看还是觉得理解的不透!
这点也是我一直疑惑的,虽然已经做了好几款PLL了
希望能有更多的人加入讨论,问题不辨不明
应该画出你的极点吧?在震荡过程中,应该很阻尼系数有关系,需要确定极点位于左半平面。
1.稳定性是对负反馈系统而言的;
2.一个基本的负反馈系统为什么会振荡?是因为负反馈变成了正反馈,且环路的放大系数大于0dB,这个时候,输出信号会无限大;
3.能提供无限信号输出的结论是从线性原理推导出来的,而实际的系统中不存在任何能提供无限大信号的器件,因此,此时的系统就转变为非线系统并振荡(如VCO,crystal osc就是利用这一点产生频率信号的),具体理论可以参看非线性系统中的极限环相关知识;
4.在我看来,任何信号都是有频率的,DC分析只是在为AC分析提供参数的一种工具,因此,对于任何系统而言,都不存在频率为0的量,因此,对于PLL而言,在零频率处相位从-180度往上走是不会不稳定的,而Nquist原理中,还有不在零频率处相位低于-180,系统也稳定的例子(只要正负穿越-180的次数可以抵消),这个还没怎么想明白和物理现象对应。
欢迎各位高手指正!
21# adelezy
这是什么tool啊?还是自己写的matlab程序啊画出来的啊?
直流的地方你说稳定不?
DC情况实际不存在
学习
haohaoxuexi
