我发现两级运放输出端看进去就是个电感
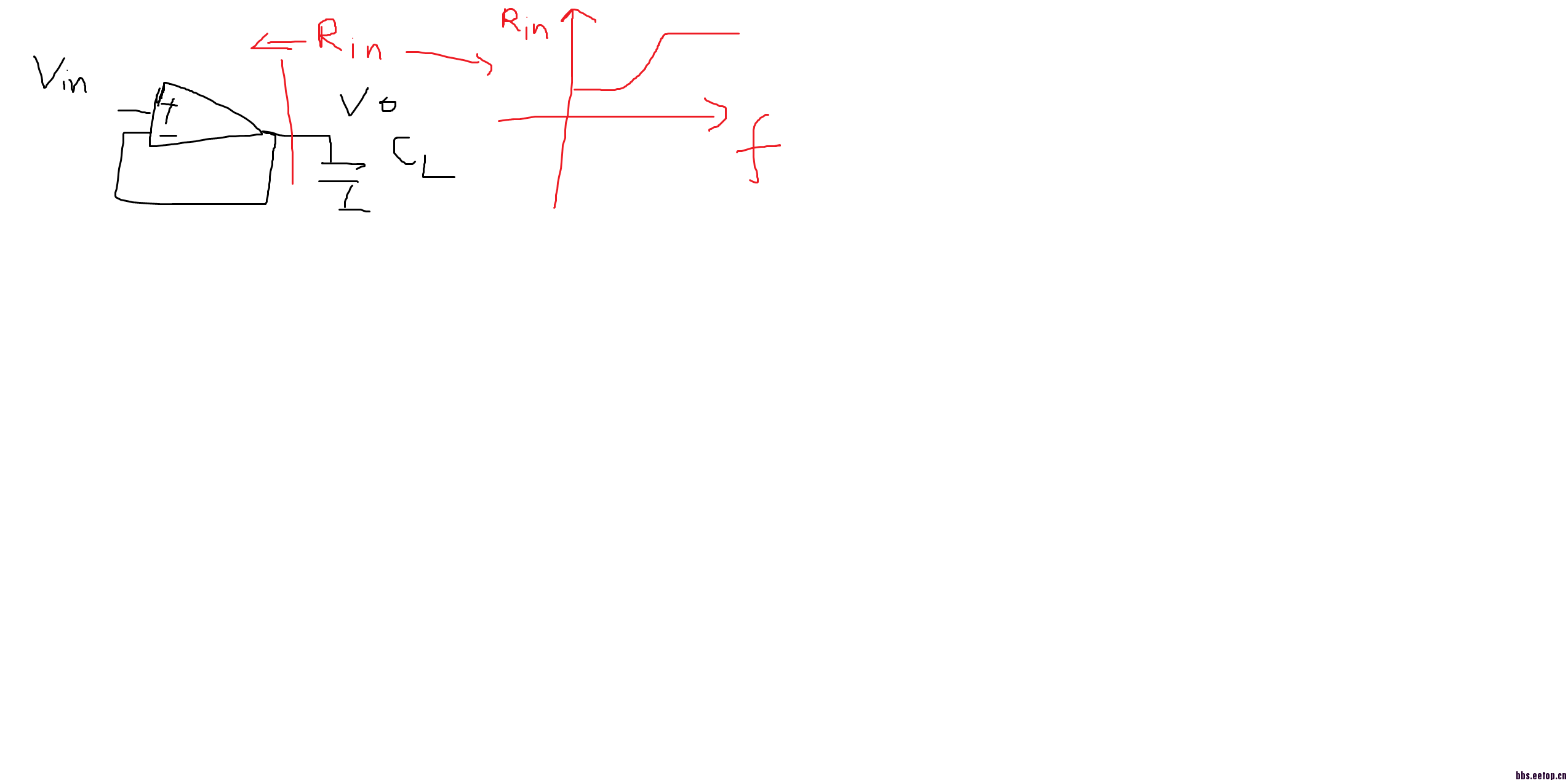
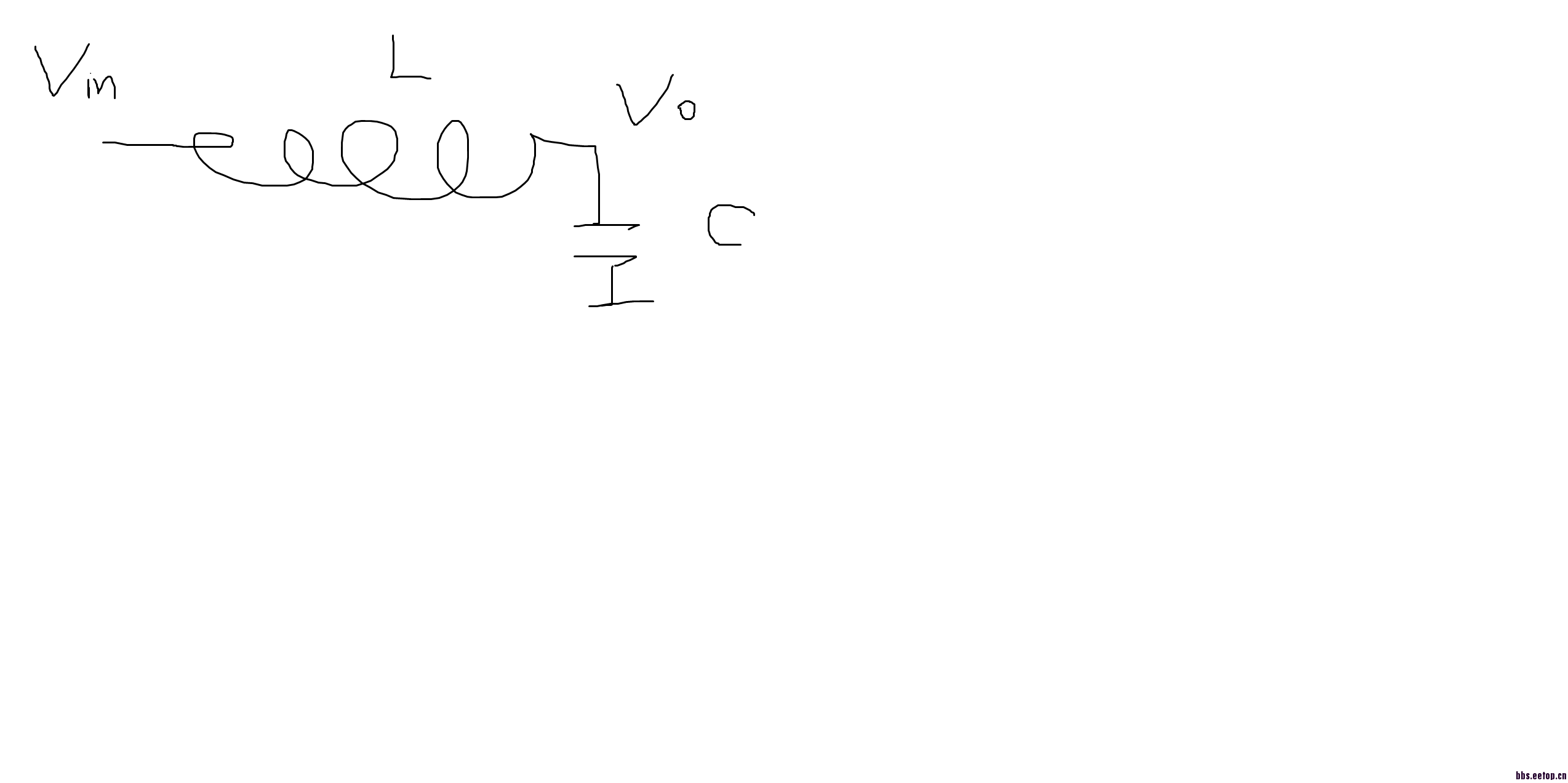
类似一个LC串联电路,输入信号加阶跃,输出电压会发生减幅振荡!
还会有CL,所以高频阻抗会下降哦
我是说除去CL之外运放输出端近似等效于一个电感。
准确的说是 OTA+C, 如果是OP的话,必须有C跨接反馈。LZ如果早出生几十年也许会发明 gm-C filter。
请问小编,单级的运放能这样看吗?那单级的运放有减幅震荡吗?你从右边看到的是这样子,而信号却从左边输入,能一样吗?
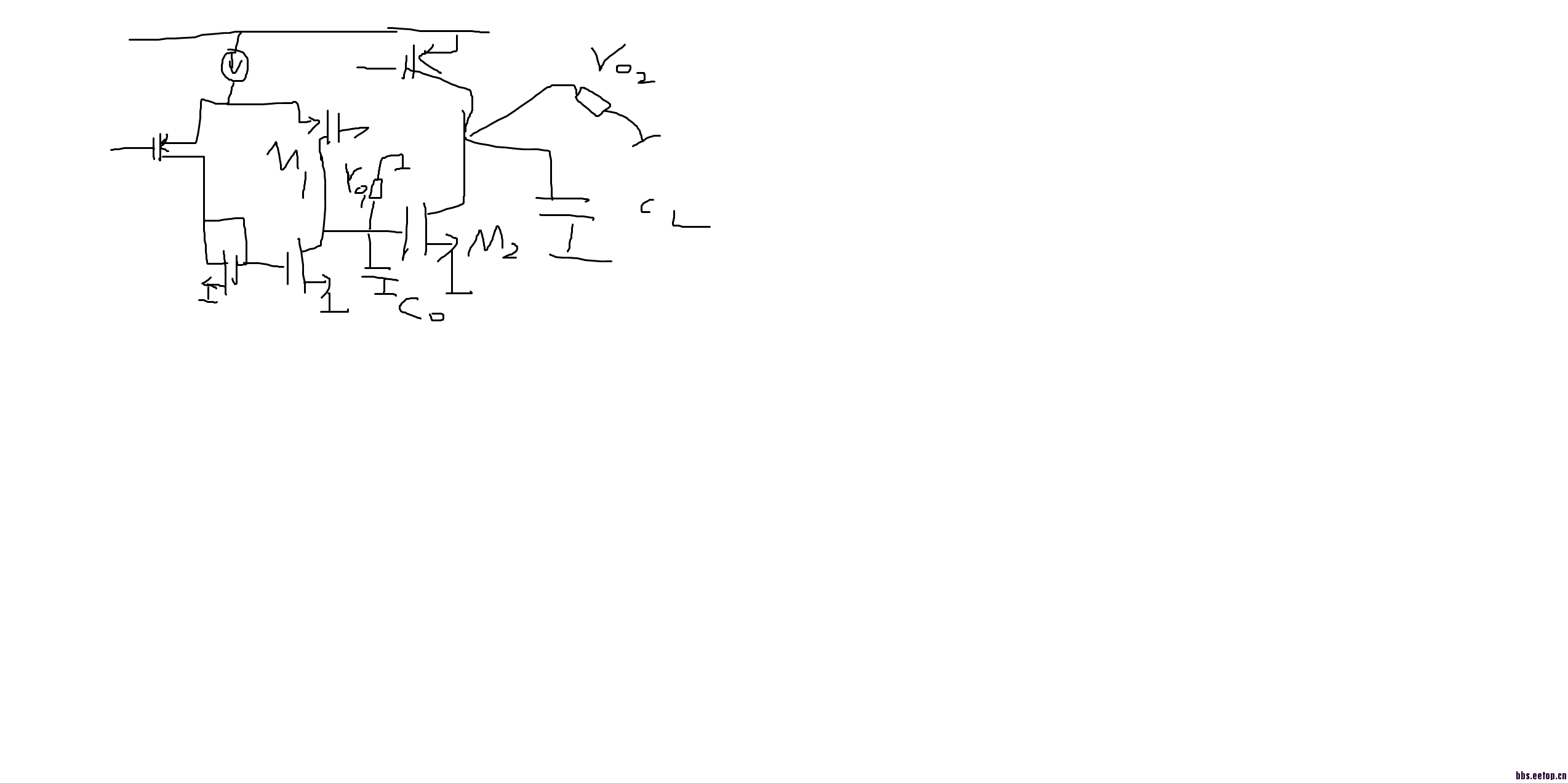
单极运放不会震荡。因为输出阻抗大约是1/gm,没有电感成分。因为运放的输出阻抗是输出级的小信号阻抗除以环路增益。单机运放输出阻抗大约是ro,环路增益是(1+Av)=(1+gmro)gm是运放输入端的跨导(五管运放为例吧),ro是输出阻抗,这样一来单机运放闭环输出阻抗是1/gm(暂时不考虑CL,因为我要计算的是Rout)。不会变高。而假设两级运放的第一级跨导是gm1,输出阻抗是ro1,第二极的跨导是gm2,输出阻抗是ro2,那么单位增益时运放闭环输出阻抗是ro2/(1+Av)=ro2/(1+gm1ro1gm2ro2),低频时约等于1/gm1ro1gm2,频率升高后,第一级增益下降,即环路增益下降,这时运放输出阻抗下降,到最后只剩下ro2与CL并肩战斗!那这样的话运放输出阻抗有电感的成分,类似于LC振荡。所以输出端会有减负振荡。
那单级运放的输出阻抗随频率升高最后不也是ro吗?为什么就不震荡呢?
单级运放输出阻抗高频时不会变为ro
求解WHY
我之前解释了啊
小编你说的两级的最后剩下ro是因为高频时环路增益下降没了;那单级的高频时环路增益照样下降没了的时候,单级的输出阻抗还是1/gm吗?
单级的时候输出阻抗是ro/(1+gmro)。无论什么时候都是这个数值,因为在计算输出阻抗的时候没有算CL。Rout和负载电容分开算了
而且我没有考虑镜像极点哈哈
那按照这个说法,两级的不算CL的话,它的阻抗就应该是1/gm2而不是ro了。ro是第二级增益也没了的时候才得到的吧,这时已经超出GBW了。
两级运放不算CL的话,由于第一级输出端有寄生电容,所以高频时第一级输出端近似接地,这样输出电阻就是ro2了。低频时第一级寄生电容开路,由于负反馈,运放闭环输出电阻是1/gm1gm2ro1.这里有电感效应,可以解释为什么两级运放会发生减幅振荡!你看看拉扎维第六章源极跟随器那一节。
哈哈,抬举了,不过拉扎维那本书真是很有意思。
典型的因为a所以b, 然后a就等于c了,最基本的thevenin equivalence先搞清楚,,,,
我觉得我的想法没错啊。输出阻抗包括一个电阻串联一个《电感与电阻并联电路》。
mark.
任意一个电路网络,传递函数的分母部分对应微分方程的齐次部分,即网络的固有响应,如果齐次微分方程的解是复数(对传递函数来说,为复数极点),固有响应即呈现衰减震荡(或连续震荡,视乎实部),在所有非vcc,gnd节点上都呈现,不仅仅在输出端!不管你是什么单级运放(它可以振荡),2级运放(它可以不振荡),等等,不管你的什么ro,cl,gm,与这些扯不上任何关系。
你可以说它等效成lc,同样可以说它等效成一根弹簧拉着一个铁球作简谐震动,因为它们的齐次微分方程的形式完全相同,核心原因就是复数根
说得好,赞一个
