带宽与相角裕度关系

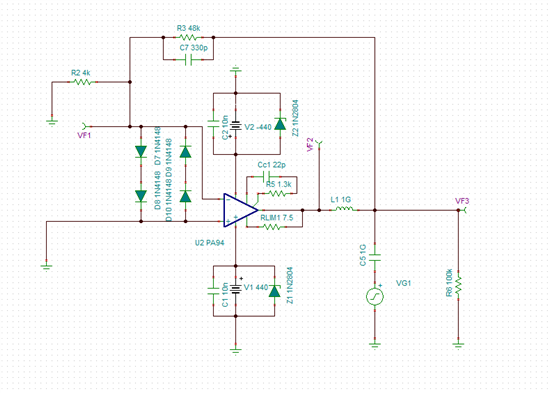
有关这个比例放大电路，上面电路是开环测试电路，用来测试电路的环路增益以及相角裕度。

当反馈网络中电容取330pF时，相角裕度为12.38°，闭环的带宽约为5kHz；

当反馈网络中电容取33pF时，相角裕度为59.78°，闭环的带宽约为200kHz。

按自动控制理论中，随着带宽的增加，相角裕度应该会随之减小才对。不知是不是我哪里理解有误。希望得到解答，非常感谢。以下是仿真文件（开环文件中已经计算好环路增益曲线AolBeta）。

8304.闭环.TSC

5852.开环.TSC

你好，相位裕度是针对开环而言的，所以看开环带宽，根据你的开环电路：

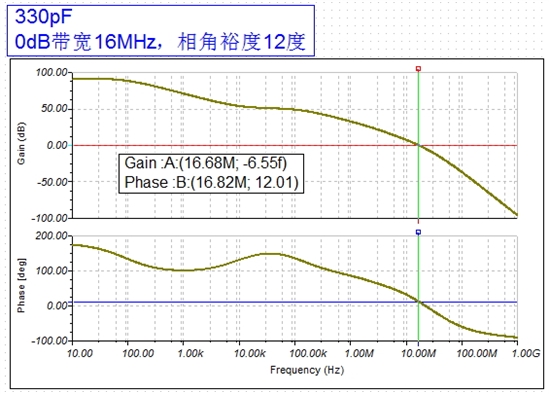
符合控制理论中带宽和相角裕度的关系。

我估计容易引起误解的地方是，因为tina的相位图是基于叠加的。所以你可以将相位理解为“相移”，因为RC的存在，直流相移为180度，所以相角裕度就是tina里所示相位和0度线的差值。

非常感谢您的回复！也就是说控制理论中带宽与相角裕度的关系指的是开环带宽与相角裕度的关系？

那我们实际应用电路的时候关心的是闭环的带宽，那对于这一放大电路，相角裕度高与闭环带宽大之间不存在矛盾？

你好，

对的。在反馈系统中：

               ------------| H |----------

             |                                     |

-------| X | ----------| G |----------------->

反馈网络H上的零极点在闭环传递函数和开环传递函数上的作用是相反的。

对开环而言：零、极点是开环传递函数 GH = 0 因式分解的分子、分母；

对闭环而言：零、极点是闭环传递函数 G/(1+GH）= 0 因式分解的分子、分母，当G很大时，其实就是 1/H = 0 的分子分母；

你可以看到，对GH=0和对1/H=0这两个数学式，H在开环上的分子（零点，相位超前）在闭环上反而成了分母（极点，相位滞后），刚好相反。

你的电路中C位于反馈网络H上，所以当你从从3.3p到330p调整C的值时，开环带宽和闭环带宽会体现出不同的变化趋势。

望知晓。

Best Regards,

Joel Li/李钊

明白了，非常感谢您的回复！