晶闸管控制感性负载,电流过零关断时的自感电动势
时间:10-02
整理:3721RD
点击:
这是很早以前的一个帖子。
原帖的内容大致是:双向晶闸管控制感性负载通断,晶闸管电流过零关断时,负载上自感电动势多大?
蚂蚁的回复大致是:自感电动势为零,因为电流为零。记忆中好像还有“哈哈”或“呵呵”的感叹。
这句话当然不对,自感电动势与电流的变化率成正比,与电流大小无关。电流为零,自感电动势未必为零。
当时想回一帖的。不过,指出这句话错误容易,要说明此瞬间及以后的自感电动势大小却需要画图,于是便放下了。这一放,就再也没有拿起来。直到看见大蚂蚁宣布找出他一个错,吃饭时他就加个菜,才又想起这件事。
原帖无图,根据原帖叙述,电路应该是如图(1)那样。
图(1)
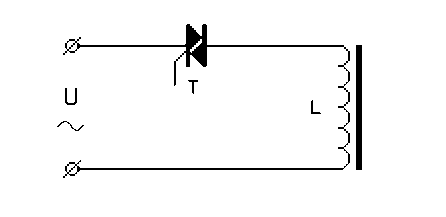
实际电路当然没有这么简单,理想电感是不存在的,绕组总有电阻和分布电容。这样,电路应该如图(2)所示,图中R为绕组的电阻,还包括铁芯的损耗和其它损耗,C为绕组的分布电容。
图(2)
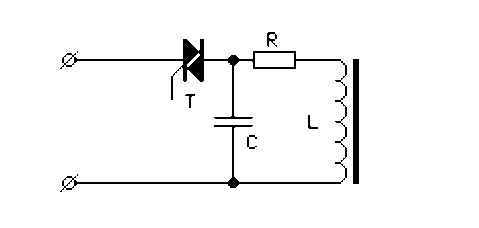
对理想电感来说,电压与电流的相位差为90度,电流落后,如图(3)。对实际电感来说,因电阻和电容的存在,电流落后于电压不到90度,但距离90度不会太远,因为电感的电阻以及电路中其它损耗还有分布电容的数值都不会很大,否则就不能说是电感性负载了。说电感性负载,实际上就是将电阻和分布电容都忽略掉不考虑的近似。
图(3)
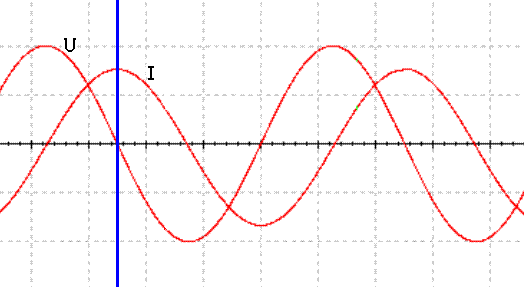
现在回到原题。原题条件是双向晶闸管电流过零关断,那么电流如图(4),蓝色圈显示了晶闸管中电流过零关断。自此瞬间之后,晶闸管中电流始终为零。
蓝色圈中电流曲线放大后如图(5)。
图(4)
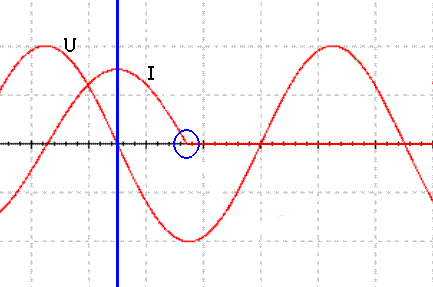
图(5)
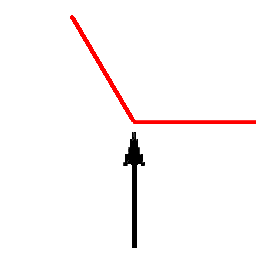
使原帖作者困惑的大概就是图(5)这条电流曲线。图中可以看到:在电流过零之前,曲线的斜率完全确定,自感电动势与电流的变化率成正比,也完全可以确定。电流过零后,始终为零,电流的变化率为零,自感电动势当然也为零。问题就在电流过零瞬间(箭头所指处)。这一点是曲线上的一个尖点,在这一点曲线没有切线,也就没有斜率,数学上叫做“不可导”或“不可微”。
蚂蚁的回复,大概也是因为看到了图(5)电流过零之后始终为零,没有变化,所以导数为零,自感电动势当然就是零。
回到原问题:既然电流在这一点(瞬间)不存在导数,那么如何确定电感负载的自感电动势?
原帖作者可能是把晶闸管中电流与负载电感中电流混淆了:图(5)是晶闸管中电流,而不是负载电感中的电流。
见图(2)。这是考虑到绕组电阻和分布电容的比图(1)更准确一些的电路。图中可见,考虑到电路中损耗和分布电容,晶闸管中电流包括电感中电流和分布电容中电流。晶闸管中电流过零,电感中电流并非是零(但很小,毕竟分布电容不大,其中电流很小)。晶闸管中电流过零,分布电容两端电压近似是交流电源电压峰值(前面已经说过,电压电流之间相位差接近90度)。
双向晶闸管关断后,电感包括其电阻以及分布电容已经与交流电源没有关系,如图(6)所示(图中仅表示绝对值)。
图(6)
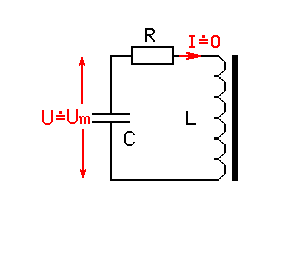
再考虑到电容两端电压不能突变,电感中的电流不能突变,我们可以有把握地说:分布电容C在晶闸管电流过零关断之后瞬间(时间间隔趋于零)两端电压等于晶闸管关断前瞬间两端电压(近似为交流电源峰值Um),电感在晶闸管电流过零关断之后瞬间(时间间隔趋于零)其中电流等于晶闸管关断前瞬间其中电流(近似为零)。
这样,问题就转化成一个没有电源的RLC电路,其初始条件是电容两端电压U近似为Um,电感中电流近似为零(所以电感中的电动势绝对值也不会超过Um)。
这样的问题,在电路分析或电路原理教材中称为“零激励二阶电路”,参见,例如,《电路原理》江缉光主编 清华大学出版社,第7章,第2节,“二阶电路的零输入响应”。
对于这样的RLC电路和初始条件,随后的电流电压变化可以求解一个常系数二阶微分方程得到。当电路中损耗很小时,电容两端电压大致如图(7)所示,是一个阻尼振荡波形,幅度逐渐减小。当电路中损耗较大时,电容两端电压波形如图(8)所示,幅度衰减得较快。当电路中损耗很大时,电容两端电压波形如图(9)所示,失去振荡特征。
图(7)
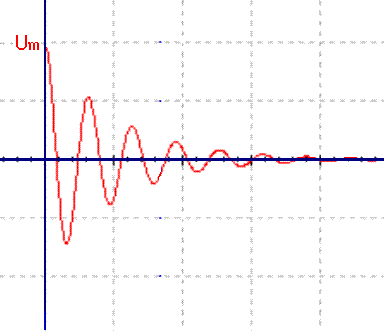
图(8)
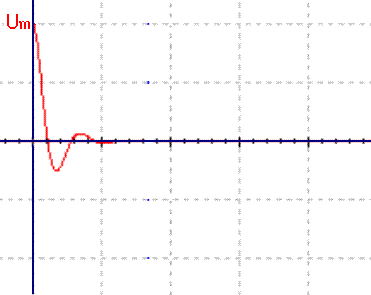
图(9)
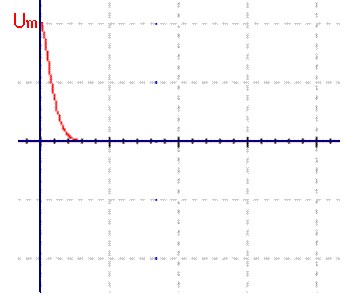
但无论是哪一种情况,电容两端电压都不会超过初始值,也就是说,不会超过Um。由此可见,电感中的电动势也不会超过Um。
从能量角度看可能更清楚。晶闸管电流过零关断瞬间,电感中电流近似为零,所以电感中并没有储存能量,分布电容中倒是储存了一定能量,大小是(C*Um^2)/2。其后能量在电感与电容之间来回交换。而每交换一次,电阻中都会损耗掉一部分。每交换一次,电容两端电压都要降低一些。损耗大时,甚至一次交换之后就全部损耗掉(图9情况)。因此关断后电感中的电动势总不会超过晶闸管电流过零关断瞬间电感中的电动势。
原帖的内容大致是:双向晶闸管控制感性负载通断,晶闸管电流过零关断时,负载上自感电动势多大?
蚂蚁的回复大致是:自感电动势为零,因为电流为零。记忆中好像还有“哈哈”或“呵呵”的感叹。
这句话当然不对,自感电动势与电流的变化率成正比,与电流大小无关。电流为零,自感电动势未必为零。
当时想回一帖的。不过,指出这句话错误容易,要说明此瞬间及以后的自感电动势大小却需要画图,于是便放下了。这一放,就再也没有拿起来。直到看见大蚂蚁宣布找出他一个错,吃饭时他就加个菜,才又想起这件事。
原帖无图,根据原帖叙述,电路应该是如图(1)那样。
图(1)

实际电路当然没有这么简单,理想电感是不存在的,绕组总有电阻和分布电容。这样,电路应该如图(2)所示,图中R为绕组的电阻,还包括铁芯的损耗和其它损耗,C为绕组的分布电容。
图(2)

对理想电感来说,电压与电流的相位差为90度,电流落后,如图(3)。对实际电感来说,因电阻和电容的存在,电流落后于电压不到90度,但距离90度不会太远,因为电感的电阻以及电路中其它损耗还有分布电容的数值都不会很大,否则就不能说是电感性负载了。说电感性负载,实际上就是将电阻和分布电容都忽略掉不考虑的近似。
图(3)

现在回到原题。原题条件是双向晶闸管电流过零关断,那么电流如图(4),蓝色圈显示了晶闸管中电流过零关断。自此瞬间之后,晶闸管中电流始终为零。
蓝色圈中电流曲线放大后如图(5)。
图(4)

图(5)

使原帖作者困惑的大概就是图(5)这条电流曲线。图中可以看到:在电流过零之前,曲线的斜率完全确定,自感电动势与电流的变化率成正比,也完全可以确定。电流过零后,始终为零,电流的变化率为零,自感电动势当然也为零。问题就在电流过零瞬间(箭头所指处)。这一点是曲线上的一个尖点,在这一点曲线没有切线,也就没有斜率,数学上叫做“不可导”或“不可微”。
蚂蚁的回复,大概也是因为看到了图(5)电流过零之后始终为零,没有变化,所以导数为零,自感电动势当然就是零。
回到原问题:既然电流在这一点(瞬间)不存在导数,那么如何确定电感负载的自感电动势?
原帖作者可能是把晶闸管中电流与负载电感中电流混淆了:图(5)是晶闸管中电流,而不是负载电感中的电流。
见图(2)。这是考虑到绕组电阻和分布电容的比图(1)更准确一些的电路。图中可见,考虑到电路中损耗和分布电容,晶闸管中电流包括电感中电流和分布电容中电流。晶闸管中电流过零,电感中电流并非是零(但很小,毕竟分布电容不大,其中电流很小)。晶闸管中电流过零,分布电容两端电压近似是交流电源电压峰值(前面已经说过,电压电流之间相位差接近90度)。
双向晶闸管关断后,电感包括其电阻以及分布电容已经与交流电源没有关系,如图(6)所示(图中仅表示绝对值)。
图(6)

再考虑到电容两端电压不能突变,电感中的电流不能突变,我们可以有把握地说:分布电容C在晶闸管电流过零关断之后瞬间(时间间隔趋于零)两端电压等于晶闸管关断前瞬间两端电压(近似为交流电源峰值Um),电感在晶闸管电流过零关断之后瞬间(时间间隔趋于零)其中电流等于晶闸管关断前瞬间其中电流(近似为零)。
这样,问题就转化成一个没有电源的RLC电路,其初始条件是电容两端电压U近似为Um,电感中电流近似为零(所以电感中的电动势绝对值也不会超过Um)。
这样的问题,在电路分析或电路原理教材中称为“零激励二阶电路”,参见,例如,《电路原理》江缉光主编 清华大学出版社,第7章,第2节,“二阶电路的零输入响应”。
对于这样的RLC电路和初始条件,随后的电流电压变化可以求解一个常系数二阶微分方程得到。当电路中损耗很小时,电容两端电压大致如图(7)所示,是一个阻尼振荡波形,幅度逐渐减小。当电路中损耗较大时,电容两端电压波形如图(8)所示,幅度衰减得较快。当电路中损耗很大时,电容两端电压波形如图(9)所示,失去振荡特征。
图(7)

图(8)

图(9)

但无论是哪一种情况,电容两端电压都不会超过初始值,也就是说,不会超过Um。由此可见,电感中的电动势也不会超过Um。
从能量角度看可能更清楚。晶闸管电流过零关断瞬间,电感中电流近似为零,所以电感中并没有储存能量,分布电容中倒是储存了一定能量,大小是(C*Um^2)/2。其后能量在电感与电容之间来回交换。而每交换一次,电阻中都会损耗掉一部分。每交换一次,电容两端电压都要降低一些。损耗大时,甚至一次交换之后就全部损耗掉(图9情况)。因此关断后电感中的电动势总不会超过晶闸管电流过零关断瞬间电感中的电动势。
分析的不错~!可是这东西有可用性吗?
学习!11
看看,好好学习
