LabVIEW双相机校准角度
在工业中很多时候我们会需要拍摄大的物体。因为物体较大,所以基本上一个相机很难拍摄完全。尤其是遇到需要求角度的时候,由于物体过大,我们基本上很难单靠一个相机抓取到一个相对稳定的角度。
而微小的角度误差,都会造成物体旋转后的偏差非常明显。这时候,我们就需要两个相机,拍摄物体两个角,然后由两边进行拟合出一条直线,算出偏移角度。这就是我们本章需要讲解的双相机校准。

这种应该也是工业应用比较广泛的案例了,但是网上什么资料或者思想也十分稀少,今天就由我抛砖引玉,给大家讲一讲我自己的方法与看法。
一.求角方法
遇到两个相机,很多人第一步想到的估计都是将两个相机转化到一个坐标系中,如果在同一个坐标系中,然后利用斜率去求出角度。还有一种是利用三角形的三边求出角度。
利用平移,我们将会得到如下图的三角形。AB和AC都是同一条边,所以AB和AC的长是相等的。而BC是在同一幅图片的,所以BC长是已知的。如果我们求出AB的长,我们即可利用三角形的正切定理求出叫a的值。
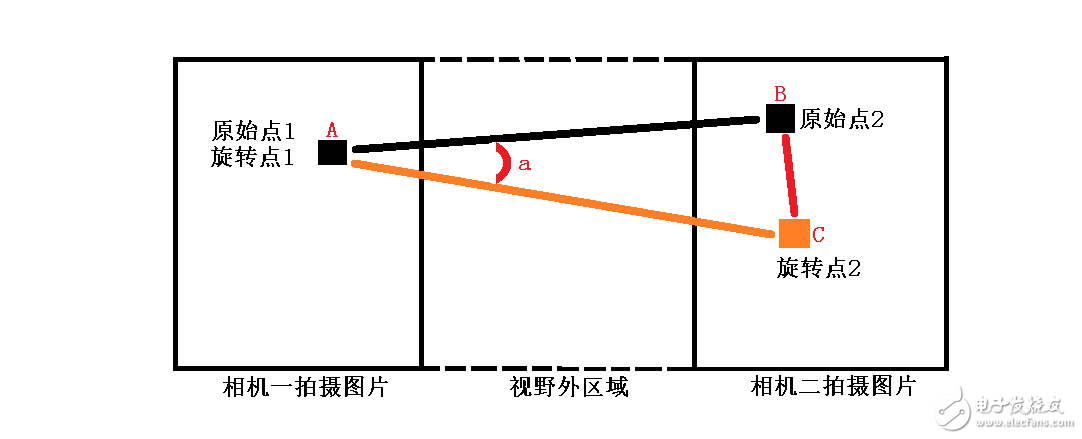
角a = 2 * arctan( AB^2 /(1/2BC))
现在,我们所剩的问题就是如何求AB边的边长了。而且求AB边边长有很多种方法,我们现在就拿两种方法来求下。
二.反向推导求边法
我们上面求边是准备利用,三角形的两边和正切定理来求的。但是,如果我们已知一条边和角度,就可以来求出我们需要的另一条边。
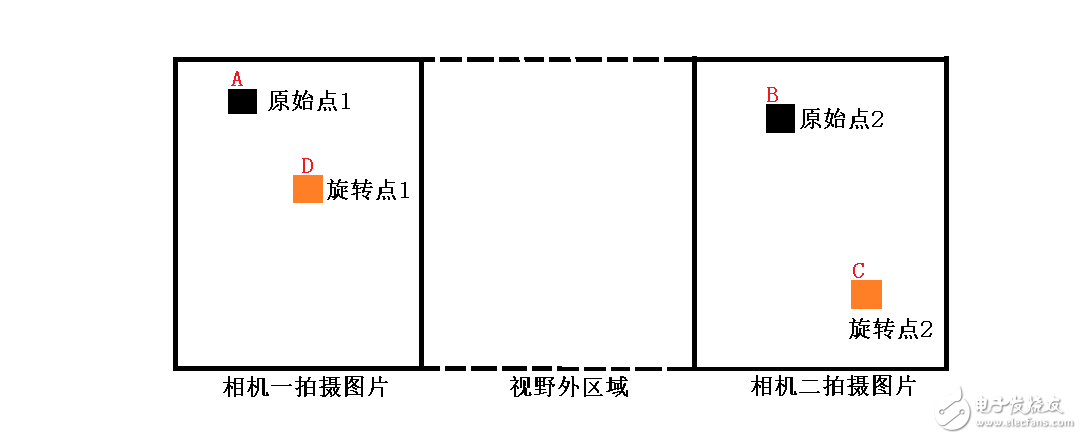
首先,我们拍摄一次得到两个点A和B。然后我们将物体旋转已知的角度,再次拍摄,我们即会得到旋转后的点,点D和点C。
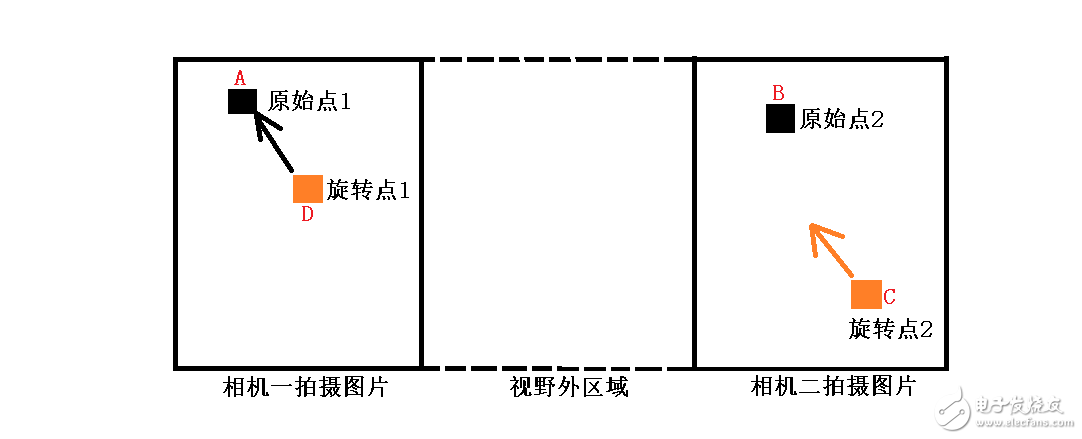
同样我们经过平移。这里要说下,两个相机的焦距可能不一样,所以我们平移的并非像素点,而是实际距离。
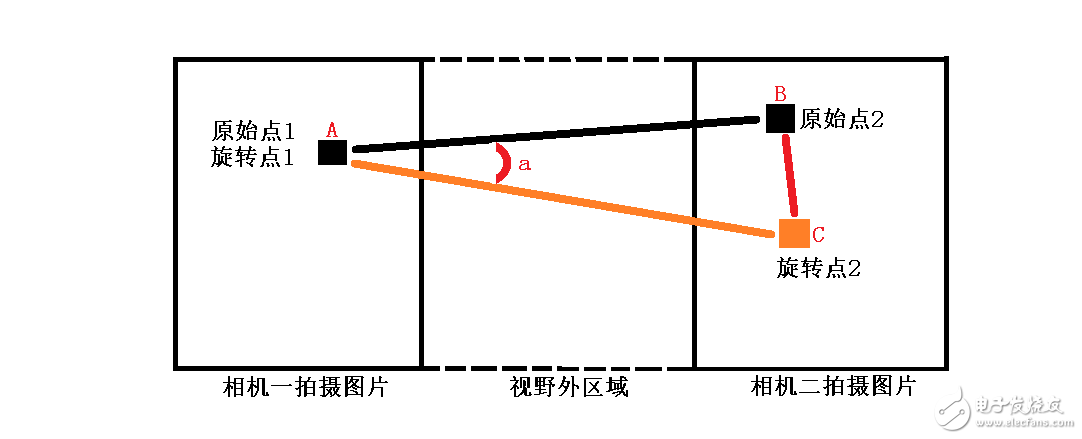
然后我们会得到下图的三角形。角a我们已知,BC我们也知晓。这时,我们利用公式 AB = 1/2BC * sin a 求出边AB。
这种方法的话,缺点就是校模板时候,手动拍摄两次。如果物体限制是比较小的,或者基本上是不能移动的,这种方法就不行了。而且每次都要旋转拍摄两次,也是比较麻烦的。
三.相对求边法
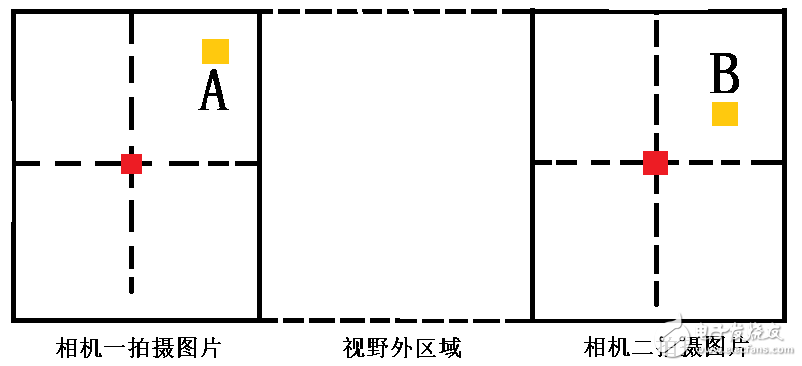
这种方法有一定的硬件限制,不过只需要拍摄一次即可。对于相机,我们要保证两个相机在同一个平面上,而且两个相机方向应该是一样的。
当相机安装好后,我们即知道两个相机中心的间距。因为相机成像的原理,相机图像的中心,就是相机中心点的投影。而且经过精确安装,我们可以保证两个相机坐标系是平行的,甚至是一样的。而相机的间距,就是两幅图片的中心点的实际距离。
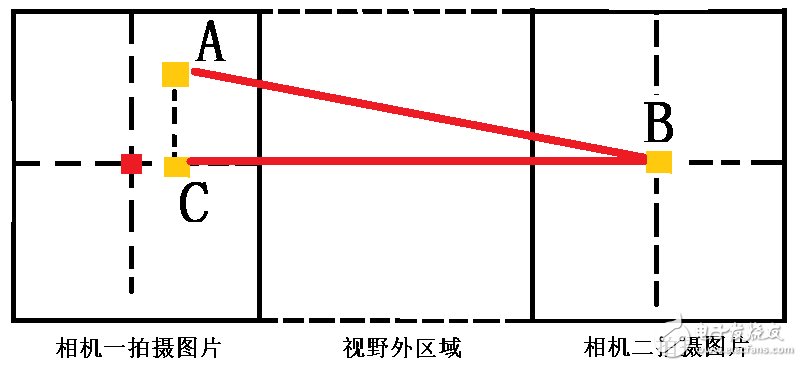
首先我们将上图B点平移到第二张图片的中心点,然后根据实际偏移,然后让A也平移B点所平移的点。然后我们将A点投影到两个中心点的连线,得到点C。
因为两中心点距离就是两相机实际距离,所以我们通过C点与中心点的偏差,我们可以求出BC的距离。而AC的距离我们也是知道的。所以已知AC和BC,我们可以根据勾股定理,求出AB的长。
AB =
四.距离确定
如果我们已知两个点距离是确定的,或者可以手动量出来,那也是可以的。这个想法还是别人问我要这距离提醒我的。缺点嘛,很明显,你要保证你拍的就是那两个特征,然后每个型号,你都要重新输下特征的数据。
因为程序只是些数学运算,就不写了,感兴趣的可以自己写下研究下。还有其实根据第二张种求边方法,我们已经可以将两幅图片转换到一幅坐标系中了。
希望今天整理的东西能够对大家思想稍微有点借鉴。同样也希望大家能够分享自己的思想,毕竟思想经过碰撞才会产生火花。
好资料 跟着小编学习了
掌声鼓励
支持,双目视觉NI给了范例不知的怎么用
小编是个大好人(大公无私)多谢!
