CST不同激励信号下的S参数
(1)默认激励信号
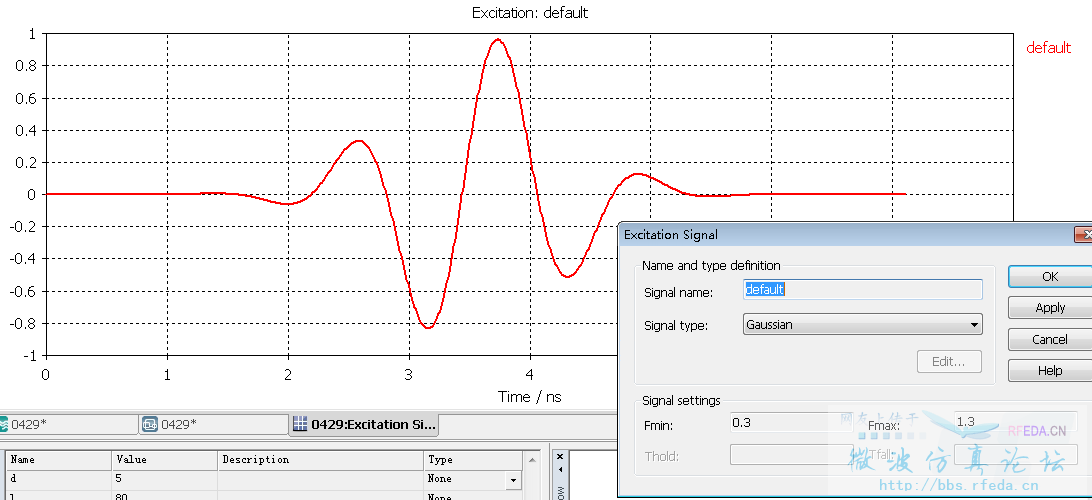
得到的S参数是这样的
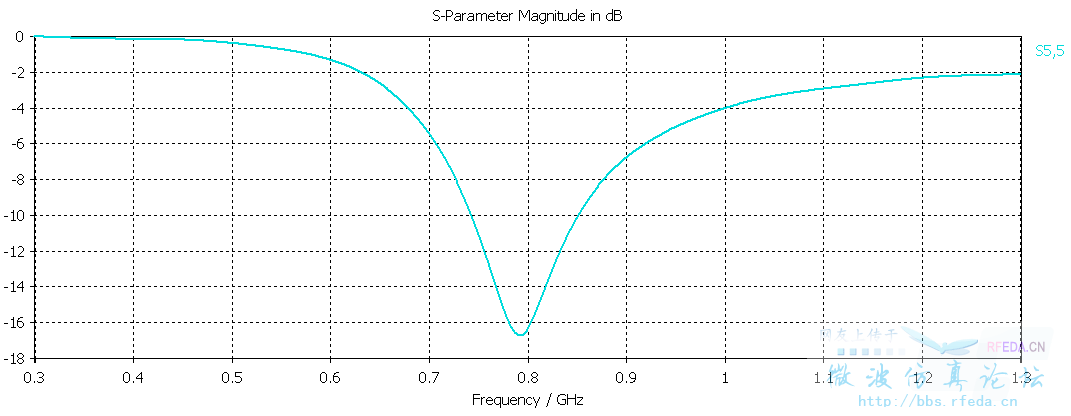
(2)正弦激励信号
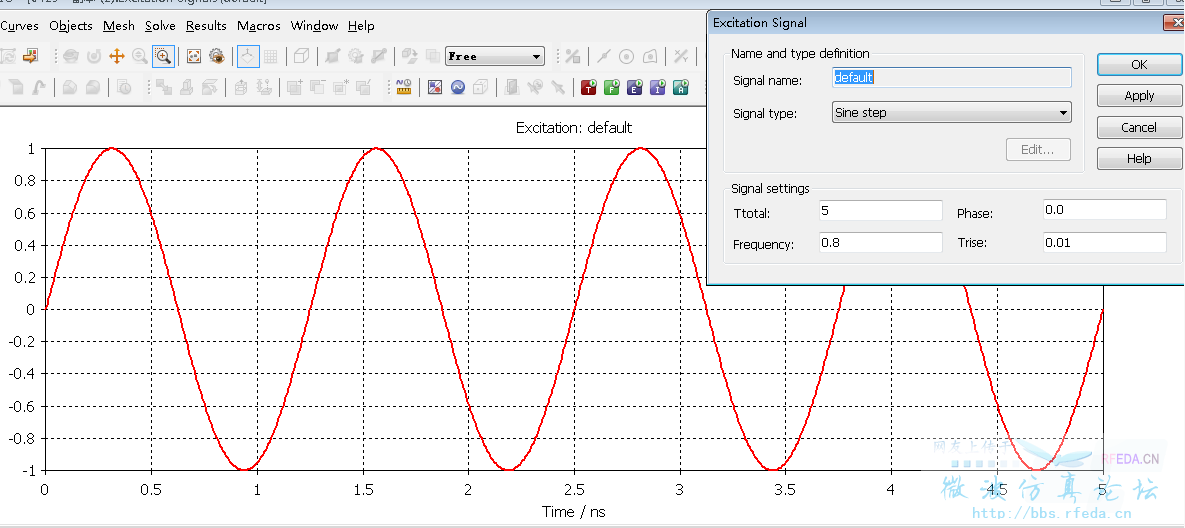
得到的S参数是这样的
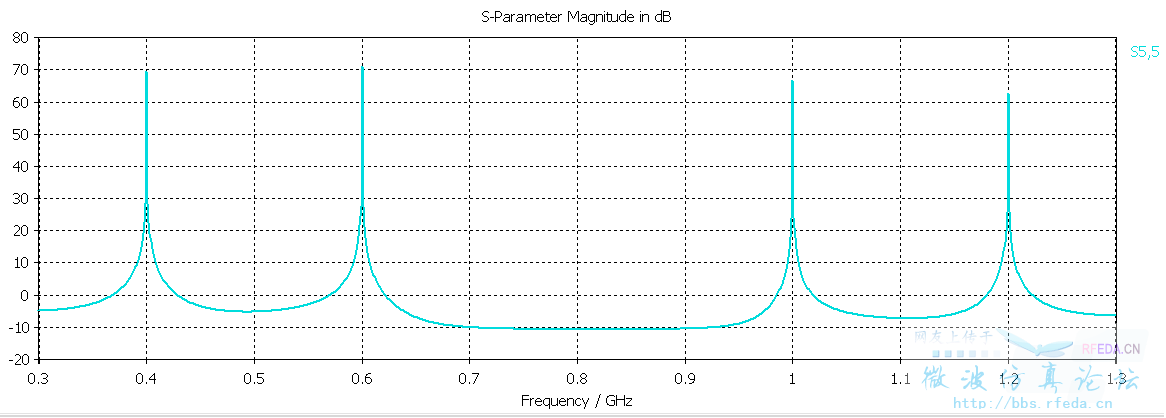
请教各位大侠(1)正弦信号里面的频率设置只是改变它的周期么?还是说仿真结果只有这个频点是靠谱的?
(2)不明白不同种类的激励信号S参数为什么差这么多,方向图差别也蛮大。我该以哪个为准呢
S参数指的是在谐波输入状态中得到的输入输出的关系。
如果分母的数字=0 你说计算的结果会靠谱吗
你只要不用正弦信号,其他的应该都靠谱都是一样的。
1、算频响要采用宽频的时域信号激励,显然正弦这种窄带信号不行
2、如果不采用CST默认的时域激励信号(gauss),如果看频响应,应设置归一化(下图)
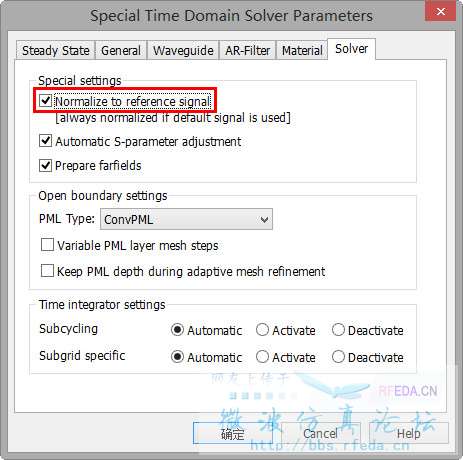
第一点好理解,
第二点中的归一化是相对于什么进行归一化?是对自己设定激励信号的最大赋值为1进行归一?其必要性是什么?不归一难道还影响S参数?这说不过去啊。
这里只需要一点基本物理常识就可以理解了。
当你要让CST算某一结构的在一定频率范围的响应情况,你有两种选择:
1. 采用频域算法(频域求解器)。对你关心的范围进行频率扫描,后处理一下就可以得到S参数与频率的关系。
2. 采用时域算法(时域求解器)。此时你虽然不需要对频率进行扫描,但这种方法对你的激励信号提出特殊的要求,算法本身我也不了解,但就我对物理本身的理解,不同信号在你关心的频率范围内的能量分布是不一样的,如果你采用频谱非常窄的信号(比如你后面那个信号),那么时域算法在很大的频率范围内都算不准(因为这些频率范围几乎没有能量)。所以你采用这种时域算法,至少保证你所选取信号的频谱覆盖所关心的频率范围。一般你设置好频率范围以后,CST自动生成一个高斯脉冲,基本可以满足前面的要求。
我觉得当运算量比较大时,时域算法相对于频域算法的优势就体现出来了。
6楼是别人回复5楼直接拷进来的?
写得很不严谨。
CST MWS帮助文件《Signals in Time Domain Simulations》。
请教,哪里理解有问题?
好吧,谢谢各位了,我大概懂了
看楼上的几位都没说出来,在CST时域仿真中,S参数是通过对时域信号进行傅里叶变换,然后相除得到的,也就是说,以S1,1为例:
S1,1=FT(o1,1)/FT(i1)
其中o1,1是端口1的反射信号,i1是端口1的输入信号(也就是激励信号),FT()表示傅里叶变换
从上面的公式就可以看出,如果i1是正弦信号,那么激励信号的频谱除了正弦频点不为0之外,其他各个频点的频谱都是0(真实仿真中由于信号长度不是无限长,所以信号频谱并不是只有一点非0,而是存在一定的带宽),导致了你用正弦激励时S参数错误的情况。
上面的公式大家完全可以使用CST自带的后处理进行验证
上面的公式也说明了为什么CST选择高斯脉冲作为激励,因为高斯脉冲在整个频段内,频谱无0点
谢谢!(说的有点迟了)
