分数N PLL相位误差产生机理及性能分析
时间:10-02
整理:3721RD
点击:
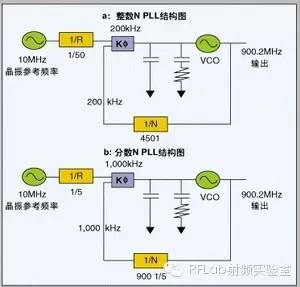
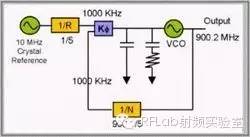
分数N锁相环(PLL)在每个递增时间都将产生一个相位误差,该相位误差将反过来产生尖峰干扰。本文分析了分数N PLL相位误差产生机理,详细介绍了采用Σ-Δ补偿降低相位误差的方法以及与整数N PLL的性能比较。 理论上,分数N PLL相对于整数N PLL具有很多优势,分数N PLL可以改善相位噪声、降低尖峰电平以及更佳的开关时间。但这些理论上的优势并不是总能在所有应用中体现出来,只有通过正确地选择合适的应用,并采用恰当的设计方法才能在实际的应用中充分利用到这些优势。分数N PLL首先了解整数N PLL。图1a是一个在要求提供信道间隙为0.2MHz、输出频率为 900.2MHz的应用中整数PLL器件的框图。将一个稳定的10MHz参考信号50倍分频来得到200kHz的比较频率,将输出频率除以4501。相位监测器K(将分频后的输出频率与比较频率(即1/R模块输出的200kHz)进行比较,并进行校正直到两个信号完全相同。将N增1达到4502,输出频率将上升0.2MHz,即信道间隙宽度。 如果能够提高N的分辨率,使之以比整数单位更小的值递增,则可以采用更低的N值,将得到更高的比较频率。采用更高的比较频率将使干扰信号进一步向更高频率转移,降低干扰信号对系统性能的影响。 图1b中的分数PLL设计为N可以整数单位的五分之一递增,即900 1/5、900 2/5、900 3/5...。将分频晶振参考的比较频率设置为1,000kHz,相对于200kHz的比较频率增大了五倍。将N设置为900 1/5,900.2MHz的期望输出频率被向下分频为1,000kHz以进行比较。将N设置为900 2/5,所期望的输出频率增加0.2MHz(即要求的信道间隙),达到900.4MHz。 分数N模数是分数1/5的分母,因为这里的分数部分可以是1/5、2/5、3/5、4/5或0,所以模数是5。由于分数PLL允许更高的比较频率,因此可以得到更大的分数模数,反过来将使尖峰信号推到更高的频率外。
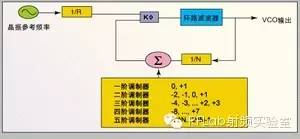
 分数N PLL相位补偿的三种方法在图1b的例子中,通过对五个比较步骤结果进行平均,分数PLL将得到一个N=900 1/5的平均值。在步骤一中,将N设置为900,分频输出频率与1,000kHz进行比较。在步骤二、三和四中,N仍然设置为900,分频输出频率与1,000kHz进行比较。但是在步骤五中,将N设置为901,将得到的分频输出频率与1,000kHz进行比较。所有五个步骤中N的平均值是900+900+900+900+901)/5 因此将得出一个900.2MHz的平均输出频率。虽然得到了900.2MHz的平均值,但在每一个递增时间(在本例中是1μs)都将产生一个相位延迟。每个相位延迟都将产生一个相位误差,反过来又产生尖峰电平(见图2)。如果相位误差没有校正或补偿的话,这些尖峰电平可能很高。有三种途径或方法来补偿引入的相位误差,前两种是模拟方法,第三种是数字方法(见图3): 方法1是一种模拟技术,在1/N模块的输出频率中引入一个时间延迟。该方法具有很强的可预测性并且在温度变化下很稳定,但是在降低尖峰的同时将增加系统相位噪声。 方法2是一种电流补偿技术,通过对发送到VCO的校正信号处理来实现,要恰当地实现这种方法具有一定困难。该方法不像方法1增加那么大的相位噪声,但是引起的尖峰很难处理。该方法的另一个问题是要求对校正电流进行频率校准,而这些值无法根据温度进行优化。 方法3切中了问题的要害,因为产生尖峰的根源是出现瞬时相位误差,该方法采用一种瞬时相位延迟校正技术来试图校正该误差。最通用的数字实现方法是采用Σ-Δ补偿。
分数N PLL相位补偿的三种方法在图1b的例子中,通过对五个比较步骤结果进行平均,分数PLL将得到一个N=900 1/5的平均值。在步骤一中,将N设置为900,分频输出频率与1,000kHz进行比较。在步骤二、三和四中,N仍然设置为900,分频输出频率与1,000kHz进行比较。但是在步骤五中,将N设置为901,将得到的分频输出频率与1,000kHz进行比较。所有五个步骤中N的平均值是900+900+900+900+901)/5 因此将得出一个900.2MHz的平均输出频率。虽然得到了900.2MHz的平均值,但在每一个递增时间(在本例中是1μs)都将产生一个相位延迟。每个相位延迟都将产生一个相位误差,反过来又产生尖峰电平(见图2)。如果相位误差没有校正或补偿的话,这些尖峰电平可能很高。有三种途径或方法来补偿引入的相位误差,前两种是模拟方法,第三种是数字方法(见图3): 方法1是一种模拟技术,在1/N模块的输出频率中引入一个时间延迟。该方法具有很强的可预测性并且在温度变化下很稳定,但是在降低尖峰的同时将增加系统相位噪声。 方法2是一种电流补偿技术,通过对发送到VCO的校正信号处理来实现,要恰当地实现这种方法具有一定困难。该方法不像方法1增加那么大的相位噪声,但是引起的尖峰很难处理。该方法的另一个问题是要求对校正电流进行频率校准,而这些值无法根据温度进行优化。 方法3切中了问题的要害,因为产生尖峰的根源是出现瞬时相位误差,该方法采用一种瞬时相位延迟校正技术来试图校正该误差。最通用的数字实现方法是采用Σ-Δ补偿。
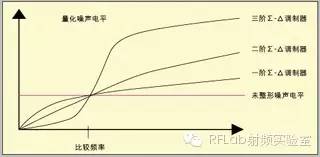
 Σ-Δ补偿降低相位误差返回去参考我们早先设置N为900 1/5的例子,一阶Σ-Δ调制器将使得在900和901之间交替变化的分数PLL获得900 1/5的平均值。二阶调制器给出四个值 (898、899、900和901),三阶调制器给出八个值(896、897、898、899、900、901、902和903)。其影响是更高阶调制器将把尖峰外推到更高的频率,如图4所示。增加Σ-Δ调制器阶数,即给调制器增加更多积分电路,也增强了图4所示的噪声整形效应(noise shaping effect)。实际上,Σ-Δ噪声整形很复杂,难以解释,最好利用Z型变压器来理解噪声整形效应是如何产生的。 更高阶调制器能够更好地将尖峰外推,但同时还外推了更多的噪声,因此需要更高阶的环型滤波器。这是因为外推得很远的噪声可能混合某些信号并以接近载波频率的尖峰返回来,因此在我们的设计中需要采用更高阶的滤波器。 等式:环型波器阶数=Σ-Δ阶数+1是采用了在环型带宽之外噪声以20dB/10倍频速率下降约束的结果。如果采用一阶调制器,那么噪声以20dB/10倍频的速率增长,因此滤波器必须以40dB/10倍频衰减。二阶滤波器在0处和T1处有一个极点,因此具有40dB/10倍频的滚降。
Σ-Δ补偿降低相位误差返回去参考我们早先设置N为900 1/5的例子,一阶Σ-Δ调制器将使得在900和901之间交替变化的分数PLL获得900 1/5的平均值。二阶调制器给出四个值 (898、899、900和901),三阶调制器给出八个值(896、897、898、899、900、901、902和903)。其影响是更高阶调制器将把尖峰外推到更高的频率,如图4所示。增加Σ-Δ调制器阶数,即给调制器增加更多积分电路,也增强了图4所示的噪声整形效应(noise shaping effect)。实际上,Σ-Δ噪声整形很复杂,难以解释,最好利用Z型变压器来理解噪声整形效应是如何产生的。 更高阶调制器能够更好地将尖峰外推,但同时还外推了更多的噪声,因此需要更高阶的环型滤波器。这是因为外推得很远的噪声可能混合某些信号并以接近载波频率的尖峰返回来,因此在我们的设计中需要采用更高阶的滤波器。 等式:环型波器阶数=Σ-Δ阶数+1是采用了在环型带宽之外噪声以20dB/10倍频速率下降约束的结果。如果采用一阶调制器,那么噪声以20dB/10倍频的速率增长,因此滤波器必须以40dB/10倍频衰减。二阶滤波器在0处和T1处有一个极点,因此具有40dB/10倍频的滚降。
 分数与整数N PLL相噪和尖峰电平比较一个常见的问题是如何比较分数和整数N PLL的相位噪声,研究发现相位噪声电平决定于信道间隙。当信道间隙很低时,分数PLL优于整数PLL。但是,当信道间隙变大时(大于200kHz),则并不总是分数PLL具有最低的相位噪声。因此,应用中的信道间隙是确定在设计中采用分数还是整数PLL的主要判据。另一个问题是如何比较不同PLL的尖峰电平。同样,在较低的信道间隙下,分数PLL优于整数PLL,因为电荷泵浦泄漏电路在整数PLL中引起额外尖峰,而分数PLL不受此影响。在10kHz到约300kHz之间的范围,一些整数PLL将优于分数PLL。但是在很高的信道间隙条件下,分数PLL又变得更好,因为其尖峰滚降比信道间隙增长更快。实际上,可以通过不采用特定的分子来进一步降低设计中的尖峰电平。但是,这要求进行良好的频率规划,并且只有具有高于100的分数模数(分数N中的分母)的PLL和更高比较频率的器件才可能实现。这在一些特殊应用中是可行的,如CDMA。 在CDMA应用中,常采用的分母是1968。研究发现,对于某些频率规划要求的最小分子是7,此时得到的分数尖峰相当低。 图5显示了通过不采用特定值作为分子的分子对尖峰的影响。例如,假设采用了一个模数为100的分数PLL,如果能够在设计中避免使用1或99做分子,则尖峰可以降低约10dB。
分数与整数N PLL相噪和尖峰电平比较一个常见的问题是如何比较分数和整数N PLL的相位噪声,研究发现相位噪声电平决定于信道间隙。当信道间隙很低时,分数PLL优于整数PLL。但是,当信道间隙变大时(大于200kHz),则并不总是分数PLL具有最低的相位噪声。因此,应用中的信道间隙是确定在设计中采用分数还是整数PLL的主要判据。另一个问题是如何比较不同PLL的尖峰电平。同样,在较低的信道间隙下,分数PLL优于整数PLL,因为电荷泵浦泄漏电路在整数PLL中引起额外尖峰,而分数PLL不受此影响。在10kHz到约300kHz之间的范围,一些整数PLL将优于分数PLL。但是在很高的信道间隙条件下,分数PLL又变得更好,因为其尖峰滚降比信道间隙增长更快。实际上,可以通过不采用特定的分子来进一步降低设计中的尖峰电平。但是,这要求进行良好的频率规划,并且只有具有高于100的分数模数(分数N中的分母)的PLL和更高比较频率的器件才可能实现。这在一些特殊应用中是可行的,如CDMA。 在CDMA应用中,常采用的分母是1968。研究发现,对于某些频率规划要求的最小分子是7,此时得到的分数尖峰相当低。 图5显示了通过不采用特定值作为分子的分子对尖峰的影响。例如,假设采用了一个模数为100的分数PLL,如果能够在设计中避免使用1或99做分子,则尖峰可以降低约10dB。
 本文小结前面提到过采用分数PLL的三个理论上的好处,包括改善的相位噪声性能和降低尖峰电平的潜力,以及改善切换时间。由于分数PLL中的尖峰比较低,可以使环路带宽更宽,这样可以改善锁定时间。实际应用中,应该把环路带宽限制到比较频率的约1/10,以避免由于离散抽样效应引起的不稳定性问题。如果比较频率低于环路带宽的100倍,则锁定时间由环路带宽唯一决定。但是,如果比较频率高于环路带宽的100倍,则会发生周期滑动(cycle slipping),影响锁定时间。因此一个潜在的缺点是,当比较频率增高时,锁定时间也增加。为了重新获得更佳的开关时间,像国家半导体公司尚未发布的分数PLL之类的器件结合了周期滑动抑制电路,测量显示当开启了抑制电路时开关速度提高了超过百分之四十。 总之,对于具有窄信道间隙的应用,分数N PLL比整数N PLL具有优势,包括更好的相位噪声规格以及降低的尖峰。但是,要注意由于比较频率增高而丧失快速的开关速度。因此,需要使用具有周期滑动抑制电路的器件。
本文小结前面提到过采用分数PLL的三个理论上的好处,包括改善的相位噪声性能和降低尖峰电平的潜力,以及改善切换时间。由于分数PLL中的尖峰比较低,可以使环路带宽更宽,这样可以改善锁定时间。实际应用中,应该把环路带宽限制到比较频率的约1/10,以避免由于离散抽样效应引起的不稳定性问题。如果比较频率低于环路带宽的100倍,则锁定时间由环路带宽唯一决定。但是,如果比较频率高于环路带宽的100倍,则会发生周期滑动(cycle slipping),影响锁定时间。因此一个潜在的缺点是,当比较频率增高时,锁定时间也增加。为了重新获得更佳的开关时间,像国家半导体公司尚未发布的分数PLL之类的器件结合了周期滑动抑制电路,测量显示当开启了抑制电路时开关速度提高了超过百分之四十。 总之,对于具有窄信道间隙的应用,分数N PLL比整数N PLL具有优势,包括更好的相位噪声规格以及降低的尖峰。但是,要注意由于比较频率增高而丧失快速的开关速度。因此,需要使用具有周期滑动抑制电路的器件。
 本文来源:NI官网
本文来源:NI官网
 分数N PLL相位补偿的三种方法在图1b的例子中,通过对五个比较步骤结果进行平均,分数PLL将得到一个N=900 1/5的平均值。在步骤一中,将N设置为900,分频输出频率与1,000kHz进行比较。在步骤二、三和四中,N仍然设置为900,分频输出频率与1,000kHz进行比较。但是在步骤五中,将N设置为901,将得到的分频输出频率与1,000kHz进行比较。所有五个步骤中N的平均值是900+900+900+900+901)/5 因此将得出一个900.2MHz的平均输出频率。虽然得到了900.2MHz的平均值,但在每一个递增时间(在本例中是1μs)都将产生一个相位延迟。每个相位延迟都将产生一个相位误差,反过来又产生尖峰电平(见图2)。如果相位误差没有校正或补偿的话,这些尖峰电平可能很高。有三种途径或方法来补偿引入的相位误差,前两种是模拟方法,第三种是数字方法(见图3): 方法1是一种模拟技术,在1/N模块的输出频率中引入一个时间延迟。该方法具有很强的可预测性并且在温度变化下很稳定,但是在降低尖峰的同时将增加系统相位噪声。 方法2是一种电流补偿技术,通过对发送到VCO的校正信号处理来实现,要恰当地实现这种方法具有一定困难。该方法不像方法1增加那么大的相位噪声,但是引起的尖峰很难处理。该方法的另一个问题是要求对校正电流进行频率校准,而这些值无法根据温度进行优化。 方法3切中了问题的要害,因为产生尖峰的根源是出现瞬时相位误差,该方法采用一种瞬时相位延迟校正技术来试图校正该误差。最通用的数字实现方法是采用Σ-Δ补偿。
分数N PLL相位补偿的三种方法在图1b的例子中,通过对五个比较步骤结果进行平均,分数PLL将得到一个N=900 1/5的平均值。在步骤一中,将N设置为900,分频输出频率与1,000kHz进行比较。在步骤二、三和四中,N仍然设置为900,分频输出频率与1,000kHz进行比较。但是在步骤五中,将N设置为901,将得到的分频输出频率与1,000kHz进行比较。所有五个步骤中N的平均值是900+900+900+900+901)/5 因此将得出一个900.2MHz的平均输出频率。虽然得到了900.2MHz的平均值,但在每一个递增时间(在本例中是1μs)都将产生一个相位延迟。每个相位延迟都将产生一个相位误差,反过来又产生尖峰电平(见图2)。如果相位误差没有校正或补偿的话,这些尖峰电平可能很高。有三种途径或方法来补偿引入的相位误差,前两种是模拟方法,第三种是数字方法(见图3): 方法1是一种模拟技术,在1/N模块的输出频率中引入一个时间延迟。该方法具有很强的可预测性并且在温度变化下很稳定,但是在降低尖峰的同时将增加系统相位噪声。 方法2是一种电流补偿技术,通过对发送到VCO的校正信号处理来实现,要恰当地实现这种方法具有一定困难。该方法不像方法1增加那么大的相位噪声,但是引起的尖峰很难处理。该方法的另一个问题是要求对校正电流进行频率校准,而这些值无法根据温度进行优化。 方法3切中了问题的要害,因为产生尖峰的根源是出现瞬时相位误差,该方法采用一种瞬时相位延迟校正技术来试图校正该误差。最通用的数字实现方法是采用Σ-Δ补偿。  Σ-Δ补偿降低相位误差返回去参考我们早先设置N为900 1/5的例子,一阶Σ-Δ调制器将使得在900和901之间交替变化的分数PLL获得900 1/5的平均值。二阶调制器给出四个值 (898、899、900和901),三阶调制器给出八个值(896、897、898、899、900、901、902和903)。其影响是更高阶调制器将把尖峰外推到更高的频率,如图4所示。增加Σ-Δ调制器阶数,即给调制器增加更多积分电路,也增强了图4所示的噪声整形效应(noise shaping effect)。实际上,Σ-Δ噪声整形很复杂,难以解释,最好利用Z型变压器来理解噪声整形效应是如何产生的。 更高阶调制器能够更好地将尖峰外推,但同时还外推了更多的噪声,因此需要更高阶的环型滤波器。这是因为外推得很远的噪声可能混合某些信号并以接近载波频率的尖峰返回来,因此在我们的设计中需要采用更高阶的滤波器。 等式:环型波器阶数=Σ-Δ阶数+1是采用了在环型带宽之外噪声以20dB/10倍频速率下降约束的结果。如果采用一阶调制器,那么噪声以20dB/10倍频的速率增长,因此滤波器必须以40dB/10倍频衰减。二阶滤波器在0处和T1处有一个极点,因此具有40dB/10倍频的滚降。
Σ-Δ补偿降低相位误差返回去参考我们早先设置N为900 1/5的例子,一阶Σ-Δ调制器将使得在900和901之间交替变化的分数PLL获得900 1/5的平均值。二阶调制器给出四个值 (898、899、900和901),三阶调制器给出八个值(896、897、898、899、900、901、902和903)。其影响是更高阶调制器将把尖峰外推到更高的频率,如图4所示。增加Σ-Δ调制器阶数,即给调制器增加更多积分电路,也增强了图4所示的噪声整形效应(noise shaping effect)。实际上,Σ-Δ噪声整形很复杂,难以解释,最好利用Z型变压器来理解噪声整形效应是如何产生的。 更高阶调制器能够更好地将尖峰外推,但同时还外推了更多的噪声,因此需要更高阶的环型滤波器。这是因为外推得很远的噪声可能混合某些信号并以接近载波频率的尖峰返回来,因此在我们的设计中需要采用更高阶的滤波器。 等式:环型波器阶数=Σ-Δ阶数+1是采用了在环型带宽之外噪声以20dB/10倍频速率下降约束的结果。如果采用一阶调制器,那么噪声以20dB/10倍频的速率增长,因此滤波器必须以40dB/10倍频衰减。二阶滤波器在0处和T1处有一个极点,因此具有40dB/10倍频的滚降。 分数与整数N PLL相噪和尖峰电平比较一个常见的问题是如何比较分数和整数N PLL的相位噪声,研究发现相位噪声电平决定于信道间隙。当信道间隙很低时,分数PLL优于整数PLL。但是,当信道间隙变大时(大于200kHz),则并不总是分数PLL具有最低的相位噪声。因此,应用中的信道间隙是确定在设计中采用分数还是整数PLL的主要判据。另一个问题是如何比较不同PLL的尖峰电平。同样,在较低的信道间隙下,分数PLL优于整数PLL,因为电荷泵浦泄漏电路在整数PLL中引起额外尖峰,而分数PLL不受此影响。在10kHz到约300kHz之间的范围,一些整数PLL将优于分数PLL。但是在很高的信道间隙条件下,分数PLL又变得更好,因为其尖峰滚降比信道间隙增长更快。实际上,可以通过不采用特定的分子来进一步降低设计中的尖峰电平。但是,这要求进行良好的频率规划,并且只有具有高于100的分数模数(分数N中的分母)的PLL和更高比较频率的器件才可能实现。这在一些特殊应用中是可行的,如CDMA。 在CDMA应用中,常采用的分母是1968。研究发现,对于某些频率规划要求的最小分子是7,此时得到的分数尖峰相当低。 图5显示了通过不采用特定值作为分子的分子对尖峰的影响。例如,假设采用了一个模数为100的分数PLL,如果能够在设计中避免使用1或99做分子,则尖峰可以降低约10dB。
分数与整数N PLL相噪和尖峰电平比较一个常见的问题是如何比较分数和整数N PLL的相位噪声,研究发现相位噪声电平决定于信道间隙。当信道间隙很低时,分数PLL优于整数PLL。但是,当信道间隙变大时(大于200kHz),则并不总是分数PLL具有最低的相位噪声。因此,应用中的信道间隙是确定在设计中采用分数还是整数PLL的主要判据。另一个问题是如何比较不同PLL的尖峰电平。同样,在较低的信道间隙下,分数PLL优于整数PLL,因为电荷泵浦泄漏电路在整数PLL中引起额外尖峰,而分数PLL不受此影响。在10kHz到约300kHz之间的范围,一些整数PLL将优于分数PLL。但是在很高的信道间隙条件下,分数PLL又变得更好,因为其尖峰滚降比信道间隙增长更快。实际上,可以通过不采用特定的分子来进一步降低设计中的尖峰电平。但是,这要求进行良好的频率规划,并且只有具有高于100的分数模数(分数N中的分母)的PLL和更高比较频率的器件才可能实现。这在一些特殊应用中是可行的,如CDMA。 在CDMA应用中,常采用的分母是1968。研究发现,对于某些频率规划要求的最小分子是7,此时得到的分数尖峰相当低。 图5显示了通过不采用特定值作为分子的分子对尖峰的影响。例如,假设采用了一个模数为100的分数PLL,如果能够在设计中避免使用1或99做分子,则尖峰可以降低约10dB。 本文小结前面提到过采用分数PLL的三个理论上的好处,包括改善的相位噪声性能和降低尖峰电平的潜力,以及改善切换时间。由于分数PLL中的尖峰比较低,可以使环路带宽更宽,这样可以改善锁定时间。实际应用中,应该把环路带宽限制到比较频率的约1/10,以避免由于离散抽样效应引起的不稳定性问题。如果比较频率低于环路带宽的100倍,则锁定时间由环路带宽唯一决定。但是,如果比较频率高于环路带宽的100倍,则会发生周期滑动(cycle slipping),影响锁定时间。因此一个潜在的缺点是,当比较频率增高时,锁定时间也增加。为了重新获得更佳的开关时间,像国家半导体公司尚未发布的分数PLL之类的器件结合了周期滑动抑制电路,测量显示当开启了抑制电路时开关速度提高了超过百分之四十。 总之,对于具有窄信道间隙的应用,分数N PLL比整数N PLL具有优势,包括更好的相位噪声规格以及降低的尖峰。但是,要注意由于比较频率增高而丧失快速的开关速度。因此,需要使用具有周期滑动抑制电路的器件。
本文小结前面提到过采用分数PLL的三个理论上的好处,包括改善的相位噪声性能和降低尖峰电平的潜力,以及改善切换时间。由于分数PLL中的尖峰比较低,可以使环路带宽更宽,这样可以改善锁定时间。实际应用中,应该把环路带宽限制到比较频率的约1/10,以避免由于离散抽样效应引起的不稳定性问题。如果比较频率低于环路带宽的100倍,则锁定时间由环路带宽唯一决定。但是,如果比较频率高于环路带宽的100倍,则会发生周期滑动(cycle slipping),影响锁定时间。因此一个潜在的缺点是,当比较频率增高时,锁定时间也增加。为了重新获得更佳的开关时间,像国家半导体公司尚未发布的分数PLL之类的器件结合了周期滑动抑制电路,测量显示当开启了抑制电路时开关速度提高了超过百分之四十。 总之,对于具有窄信道间隙的应用,分数N PLL比整数N PLL具有优势,包括更好的相位噪声规格以及降低的尖峰。但是,要注意由于比较频率增高而丧失快速的开关速度。因此,需要使用具有周期滑动抑制电路的器件。  本文来源:NI官网
本文来源:NI官网
