信号处理中伟大的傅里叶变换(可能的话高中生都能看懂...
写在最前,这是摘自《神奇的矩阵第二季》爱上积分变换那一节。有关傅里叶
傅里叶分析不仅仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。但不幸的是,傅里叶分析的公式看起来太复杂了,所以很多大一新生上来就懵圈并从此对它深恶痛绝。
老实说,这么有意思的东西居然成了大学里的杀手课程,不得不归咎于编教材的人实在是太严肃了。所以我一直想写一个有意思的文章来解释傅里叶分析,有可能的话高中生都能看懂的那种。所以,不管读到这里的您从事何种工作,我保证您都能看懂,并且一定将体会到通过傅里叶分析看到世界另一个样子时的快感。至于对于已经有一定基础的朋友,也希望不要看到会的地方就急忙往后翻,仔细读一定会有新的发现。
傅里叶是一位法国数学家和物理学家的名字,英语原名是Jean Baptiste Joseph Fourier(1768-1830), Fourier对热传递很感兴趣,于1807年在法国科学学会上发表了一篇论文,运用正弦曲线来描述温度分布,论文里有个在当时具有争议性的决断:任何连续周期信号可以由一组适当的正弦曲线组合而成。
当时审查这个论文的人,其中有两位是历史上著名的数学家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯(Pierre Simon de Laplace, 1749-1827),当拉普拉斯和其它审查者投票通过并要发表这个论文时,拉格朗日坚决反对,在他此后生命的六年中,拉格朗日坚持认为傅里叶的方法无法表示带有棱角的信号,如在方波中出现非连续变化斜率。法国科学学会屈服于拉格朗日的威望,拒绝了傅里叶的工作,幸运的是,傅里叶还有其它事情可忙,他参加了政治运动,随拿破仑远征埃及,法国大革命后因会被推上断头台而一直在逃避。直到拉格朗日死后15年这个论文才被发表出来。
拉格朗日是对的:正弦曲线无法组合成一个带有棱角的信号。
但是,我们可以用正弦曲线来非常逼近地表示它,逼近到两种表示方法不存在能量差别,基于此,傅里叶是对的。
话是这么说没错,可是二者总要存在差异,甚至在跳变沿处,傅里叶逼近会产生Gibbs现象,我们为什么还要进行傅里叶展开或傅里叶变换呢?

首先,我们从物理系统的特征信号角度来解释。
我们知道,大自然中很多现象可以抽象成一个线性时不变系统来研究,无论你用微分方程还是传递函数或者状态空间描述。
线性时不变系统可以这样理解:
输入输出信号满足线性关系,而且系统参数不随时间变换。对于大自然界的很多系统,一个正弦曲线信号输入后,输出的仍是正弦曲线,只有幅度和相位可能发生变化,但是频率和波的形状仍是一样的。
也就是说正弦信号是系统的特征向量!当然,指数信号也是系统的特征向量,表示能量的衰减或积聚。自然界的衰减或者扩散现象大多是指数形式的,或者既有波动又有指数衰减(复指数形式),因此具有特征的基函数就由三角函数变成复指数函数。但是,如果输入是方波、三角波或者其他什么波形,那输出就不一定是什么样子了。所以,除了指数信号和正弦信号以外的其他波形都不是特征信号。


怎么理解我所说的特征向量和特征信号这个名字呢?其实这来源于线性代数:我们知道矩阵A作用一个特征向量x可以用数学语言这样描述:,那么系统作用一个特征信号用数学语言描述就是。形式结构相同,只是一个是有限长度的向量,另一个是无限长度的信号而已。既然是特征向量,我们就想能不能用特征向量来表示自然界的信号和一个物理系统呢?这样做的好处就是知道输入,我们就能很简单那的写出输出。我们来看一个实际的例子,击弦乐器——钢琴。琴键被小锤敲击后,产生声音,见下图。
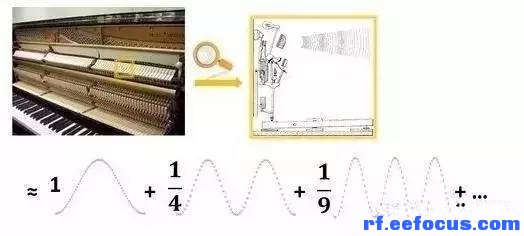
你可以认为声音是琴键随时间变化的,也可以看成是各种波的叠加。用数学的表达式就是这个样子的:

凡有变化的波(交流、频率)才能传递信号,一个一直不变的直流信号是无法传递信息的。这种“交流”是指广义的,普遍的,无论是自然界里蝙蝠探路,人们互相交谈,还是卫星接收信号,都属于交流的范畴。
为了传递信号,产生交流,我们需要以“波”作为信号的载体。最简单的波,就以一定频率传播。蝙蝠发出了超声波,人们说话,声带振动带动了空气疏密波(声波),卫星识别电磁波。这样,我们就有了频率的概念。更进一步,除了手机GHz的波这些经典电磁波,在量子世界里,原子的跃迁也是以一定的频率发生的。我们甚至可以说,自然选择了以这些单频的模式为基础。对于一个信号来说,信号强度随时间的变化规律就是时域特性,信号是由哪些单一频率的信号合成的就是频域特性。
为什么时间和频率描述世界是等价的这里引入了时域频域的概念。我们就有必要解释一下为什么时间和频率来描述这个世界是等价的?
什么是时域?从我们出生,我们看到的世界都以时间贯穿,股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为,世间万物都在随着时间不停的改变,并且永远不会静止下来。
什么是频域?频域(frequency domain)是描述信号在频率方面特性时用到的一种坐标系。用线性代数的语言就是装着正弦函数的空间。频域最重要的性质是:它不是真实的,而是一个数学构造。频域是一个遵循特定规则的数学范畴。正弦波是频域中唯一存在的波形,这是频域中最重要的规则,即正弦波是对频域的描述,因为时域中的任何波形都可用正弦波合成。
好抽象,不懂。那让我们从一个简单的例子开始吧。在你的理解中,一段音乐是什么呢?
这是我们对音乐最普遍的理解,一个随着时间变化的震动。但我相信对于乐器小能手们来说,音乐更直观的理解是这样的:

最上面的图是音乐在时域的样子,而下面的图则是音乐在频域的样子。所以频域这一概念对大家都从不陌生,只是从来没意识到而已。
其实,在生活中,我们无时无刻不在进行着傅立叶变换。(什么?我没有听错吧?!)对的,请相信你的耳朵,你完全没有听错。我们来看人类听觉系统的处理过程:
当我们听到一个声音,大脑的实际反应是什么?事实上耳朵感觉到一个时变的空气压力,这种变化也许是一个类似于口哨声的单音。当我们听到一个口哨声时,我们所关心的并不是气压随时间的振动(它非常非常快!),而是声音的三个特征:基音、声强以及音长。基音可以理解为频率的同义词,声强不是别的,它就是幅度。我们的耳朵—大脑系统能有效地将信号表示成三个简单的特征参数:基音、声强以及音长,并不理会气压的快速变化过程(一个重复的变化过程)。这样耳朵—大脑系统就提取了信号的本质信息。
傅立叶变换的分析过程与此类似,只不过我们从数学意义把它更加精确化和专业话罢了。
从数学上理解,频域的概念就是由正弦信号构成的空间。或者说这个空间里装着正弦信号。听起来好抽象,让我们回忆一个例子:我们知道对已一个函数,我们可以将它分解成下面的形式:
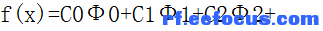
分解的方法有很多。
我们这样理解上面的函数分解:是函数空间中的一组基,是在这组基下的坐标。对于泰勒展开,我们选取了多项式作为基,于是由多项式构成的空间就叫多项式空间。对于傅里叶变换,我们只是选取了三角函数作为基,于是由三角函数构成的空间就叫频率空间或者叫频域。以此类推。
用正弦曲线来代替原来的曲线而不用方波或三角波或者其他什么函数来表示的原因在于:正弦信号恰好是很多线性时不变系统的特征向量。于是就有了傅里叶变换。对于更一般的线性时不变系统,复指数信号(表示耗散或衰减)是系统的“特征向量”。于是就有了拉普拉斯变换。z变换也是同样的道理,这时是离散系统的“特征向量”。这里没有区分特征函数和特征向量的概念,主要想表达二者的思想是相同的,只不过一个是有限维向量,一个是无限维函数。
傅里叶级数和傅里叶变换其实就是我们之前讨论的特征值与特征向量的问题。分解信号的方法是无穷的,但分解信号的目的是为了更加简单地处理原来的信号。这样,用正余弦来表示原信号会更加简单,因为正余弦拥有原信号所不具有的性质:正弦曲线保真度。且只有正弦曲线才拥有这样的性质。
同时,这也解释了为什么我们一碰到信号就想方设法的把它表示成正弦量或者复指数量的形式;解释了为什么方波或者三角波如此“简单”,我们非要展开的如此“麻烦”;解释了为什么对于一个没有什么规律的“非周期”信号,我们都绞尽脑汁的用正弦量展开。就因为正弦量(或复指数)是特征向量。
考虑到实际过程都只关心t>0时刻的现象,所以一般用的拉氏变换都是单边的,也就是教材中讲的拉普拉斯变换。微分运算的变换,除了以外还有其它项,就是因为所做的是单边的变换,需要考虑初值。
时域分析与频域分析是对信号的两个观察面。时域分析是以时间轴为坐标表示动态信号的关系;频域分析是把信号变为以频率轴为坐标表示出来。一般来说,时域的表示较为形象与直观,频域分析则更为简练,剖析问题更为深刻和方便。目前,信号分析的趋势是从时域向频域发展。然而,它们是互相联系,缺一不可,相辅相成的。贯穿时域与频域的方法之一,就是传中说的傅里叶分析。傅里叶分析可分为傅里叶级数(Fourier Serie)和傅里叶变换(Fourier Transformation)。
鉴于你对积分变换已经心灰意冷,为了让你对积分变换产生一点好感。我们来看一张图:
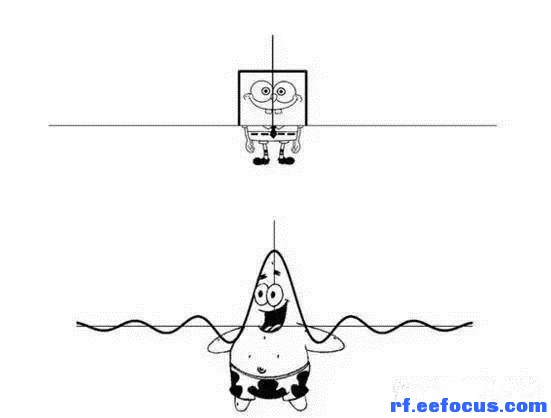
海绵宝宝的傅里叶变换就是派大星
这个图在讨论滤波器的时候很有用,学习通讯或者电子专业的学生对这个图再熟悉不过了,如果你感兴趣可以联系我交流一下。
之前说了那么多,可能你不相信一个信号可以用正弦信号的线性组合重现,或者说你不相信一个函数可以展开。接下来,我们深入的讨论一下这个问题。

什么是分解呢?分解的意思就像我们用不同的涂料来调色,一个色调可以分解成不同基色调的组合。一束白光可以分解成不同颜色的光的叠加。如果我说我能用前面说的正弦曲线波叠加出一个带90度角的矩形波来,你会相信吗?你不会,就像当年的我一样。但是看看下图:



随着叠加的递增,所有正弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡,而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分使其变为水平线。一个矩形就这么叠加而成了。但是要多少个正弦波叠加起来才能形成一个标准90度角的矩形波呢?不幸的告诉大家,答案是无穷多个。用线性代数的角度来说明这个问题,就是基的数量要足够,数学一点的用语是完备性。如果你接触过小波变换,你就更能体会到这点。
不仅仅是矩形,你能想到的任何波形都是可以如此方法用正弦波叠加起来的。这是没有接触过傅里叶分析的人在直觉上的第一个难点,但是一旦接受了这样的设定,游戏就开始有意思起来了。
(2012年1月,四位来自麻省理工学院的研究人员提出了一种更快执行傅里叶变换的新算法。这四位研究者(从左至右)分别是Piotr Indyk、Dina Katabi、Eric Price、Haitham Hassanieh。傅里叶变换是数字医学成像、Wi-Fi路由器和4G无线通信网络等众多技术的运算基础。)
经过上面各种图形的狂轰滥炸,相信你对于傅里叶级数是展开(分解)的概念已经在你的脑海中留下一些痕迹了吧。前面的叠加过程我们发现随着频率越来越高,幅值却越来越小。这是为什么呢?很多书上只是给出数学上的解释。下面,给出一个几何上的解释:

对于一个函数,将其分解成傅里叶级数的时候,对于高频分量,可以看出函数近似成一条直线。于是,积分求和就变成很小的值了。这也是为什么工程中只取前几阶信号而不考虑无穷项的原因。
前面花了大量的时间来说明一个方波信号可以由正弦信号组成,也就是一个时域信号可以用频域信号表示。如果你接受了这件事,就好办了,我们将他推广:
“任意连续周期信号可以由一组适当的正弦曲线组合而成”
这就是傅里叶当年的结论。
尽管最初傅里叶分析是作为热过程的解析分析的工具,但是其思想方法仍然具有典型的还原论和分析主义的特征。”任意”的函数通过一定的分解,都能够表示为正弦函数的线性组合的形式,而正弦函数在物理上是被充分研究而相对简单的函数类,这一想法跟化学上的原子论想法何其相似!
本节的核心就是一种信号可以用另一种信号作为基函数线性表示。而由于现实世界中正弦信号是系统的特征向量,所以我们就用傅里叶变换,将研究的信号在频域展开。总而言之,不管是傅里叶级数,还是傅里叶变换、拉普拉斯变换、z变换,本质上都是线性代数里面讲的求特征值和特征向量。然后将一个复杂问题用特征值和特征向量表示。以后如果有人问你为什么要进行傅里叶变换,你就可以半炫耀半学术的告诉他:
“因为复指数信号是线性时不变系统的特征向量,因此傅里叶变换就是进行特征分解”
当然还有其他展开,比如小波,道理是一样的。如果感兴趣,强烈推荐《小波与傅里叶分析基础》这本书。
其实写到这里本来就可以了。但是数学家觉得,这种向特征基函数投影的思想太奇妙了,于是就将其发展延伸,构造出了其他形式的积分变换。下面就从数学的角度解释一下积分变换的意义。
从数学角度解析傅里叶变换的意义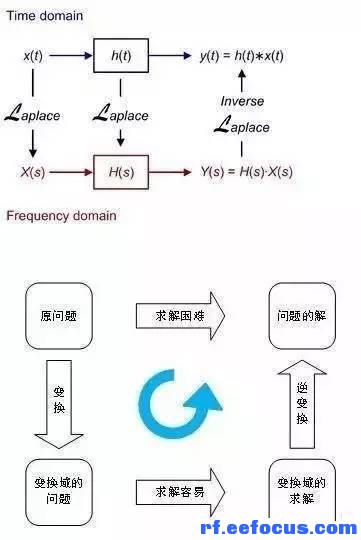
这种解决问题的思路和我们介绍的对角化时的思路是一致的。类似的还有对数变换、解析几何的坐标变换、高等代数中的线性变换;在积分中的变量代换和积分运算化简;在微分方程中所作的自变量或未知函数的变换;复变函数的保角变换。当然变换要可以逆。也就是下面介绍的核函数要可逆。
从数学的角度理解积分变换就是通过积分运算,把一个函数变成另一个函数。也可以理解成是算内积,然后就变成一个函数向另一个函数的投影:

K(s,t)是积分变换的核(Kernel)。当选取不同的积分域和变换核时,就得到不同名称的积分变换。学术一点的说法是:向核空间投影,将原问题转化到核空间。所谓核空间,就是这个空间里面装的是核函数。下表列出常见的变换及其核函数:

当然,选取什么样的核主要看你面对的问题有什么特征。不同问题的特征不同,就会对应特定的核函数。把核函数作为基函数。将现在的坐标投影到核空间里面去,问题就会得到简化。之所以叫核,是因为这是最核心的地方。为什么其他变换你都没怎么听说过而只熟悉傅里叶变换和拉普拉斯变换呢?因为复指数信号才是描述这个世界的特征函数!
写到这里,我觉得早晚会有人指出我的一个问题:没有区分傅里叶级数和傅里叶变换。笔者觉得这两个概念根本没必要区分,我的理由如下:傅里叶级数和傅里叶变换的根本区别是被操作的函数是否为周期函数:当被操作函数的周期趋向于无穷大,傅里叶级数“密集”成傅里叶变换;当被操作函数的周期从无穷大变成有限值时,傅里叶变换退化成傅里叶级数。所以,其实傅里叶级数只是傅里叶变换的一种特殊情况,或者说傅里叶变换是傅里叶级数的推广。因此,笔者不希望用高深繁多的概念来把你搞晕,就没有强调二者的区别。

当然,这个问题还体现了时频域之间的对称(对偶)关系,而且对拉普拉斯变换也适用,请看下表:

举个例子:

比如你在时域周期延拓,那么频域就是离散的线谱;你在时域离散(采样),那么频域就是周期的。还记得海绵宝宝和派大星那个图么?时域的窗函数在频域就是sinc函数;频域的窗函数(理想低通滤波器)在时域就是sinc函数。因此,由于非因果性,理想低通滤波器是不存在的。当然,有些公式并不严谨,只是为了形式上的好看,希望你谅解。详细而准确的推导请参考积分变换或者信号与系统类的书籍。
现代数学发现傅里叶变换具有非常好的性质,使得它如此的好用和有用,让人不得不感叹造物的神奇:
- 傅里叶变换是线性算子,若赋予适当的范数,它还是酉算子;
- 傅里叶变换的逆变换容易求出,而且形式与正变换非常类似;
- 正弦基函数是微分运算的本征函数,从而使得线性微分方程的求解可以转化为常系数的代数方程的求解。在线性时不变的物理系统内,频率是个不变的性质,从而系统对于复杂激励的响应可以通过组合其对不同频率正弦信号的响应来获取;
- 著名的卷积定理指出:傅里叶变换可以化复杂的卷积运算为简单的乘积运算,从而提供了计算卷积的一种简单手段;
- 离散形式的傅里叶变换可以利用数字计算机快速的算出(其算法称为快速傅里叶变换算法(FFT)).
正是由于上述的良好性质,傅里叶变换在物理学、数论、组合数学、信号处理、概率、统计、密码学、声学、光学等领域都有着广泛的应用。
文章写得不错啊,给赞
有种瞬间眼前一亮的感觉都不夸张
深入浅出的讲解,当时的老师这样讲课,估计就不会有那么多挂科的吧?
